0.2 Is What Percent Of 16
Treneri
May 11, 2025 · 4 min read
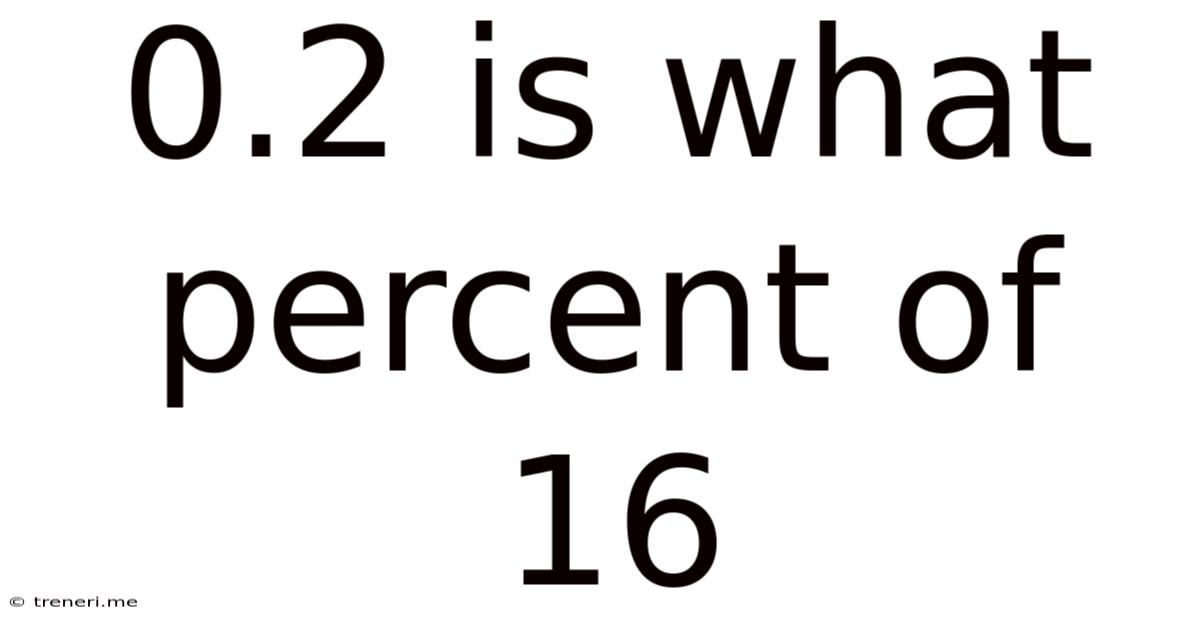
Table of Contents
0.2 is What Percent of 16? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analyses. This article delves deep into the calculation of "0.2 is what percent of 16," providing a step-by-step solution, exploring different approaches, and expanding on the broader concept of percentages. We’ll also examine practical applications and provide you with the tools to confidently solve similar percentage problems.
Understanding Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Method 1: Using Proportions
This method is arguably the most intuitive way to solve percentage problems. We can set up a proportion to represent the relationship between the parts and the whole:
Part / Whole = Percentage / 100
In our case:
- Part: 0.2
- Whole: 16
- Percentage: This is what we need to find (let's represent it with 'x')
Therefore, our proportion becomes:
0.2 / 16 = x / 100
To solve for 'x', we cross-multiply:
0.2 * 100 = 16 * x
20 = 16x
Now, divide both sides by 16:
x = 20 / 16
x = 1.25
Therefore, 0.2 is 1.25% of 16.
Method 2: Using Decimal Conversion
This method involves converting the percentage to a decimal and then solving the equation. We know that 'x%' can be represented as x/100. So, our problem can be rewritten as:
0.2 = (x/100) * 16
To solve for 'x', we can follow these steps:
- Divide both sides by 16: 0.2 / 16 = x / 100
- Simplify the left side: 0.0125 = x / 100
- Multiply both sides by 100: 0.0125 * 100 = x
- Solve for x: x = 1.25
Again, we arrive at the same answer: 0.2 is 1.25% of 16.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function (%) that directly handles these types of problems. Simply enter "0.2 ÷ 16 × 100 =" The result will be 1.25. This method is efficient and reduces the chance of calculation errors.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage computations. Understanding percentages is crucial for making informed financial decisions.
-
Science: Percentage change is commonly used to express changes in data, such as population growth, experimental results, and chemical concentrations.
-
Retail: Sales discounts, markups, and profit margins are expressed as percentages. Customers and retailers use these percentages to understand pricing strategies and potential savings.
-
Statistics: Percentages are fundamental to statistical analysis for expressing proportions, probabilities, and confidence intervals.
-
Everyday Life: Calculating tips, understanding nutritional information (percentage of daily value), and interpreting survey results all involve working with percentages.
Expanding on Percentage Problems: Variations and Challenges
While the problem "0.2 is what percent of 16" provides a good foundation, let's explore more complex scenarios:
1. Finding the Whole: What if the problem was "0.2 is 1.25% of what number?" To solve this, we would rearrange our proportion:
Part / Whole = Percentage / 100
0.2 / x = 1.25 / 100
Cross-multiplying and solving for x gives us x = 16. This confirms our initial problem.
2. Finding the Part: What if the problem was "1.25% of 16 is what number?" This is a direct percentage calculation: (1.25/100) * 16 = 0.2
3. Percentage Increase/Decrease: Problems involving percentage increase or decrease require a slightly different approach. For example: "A price increased by 10% from $100. What is the new price?" This involves calculating the increase (10% of $100 = $10) and adding it to the original price ($100 + $10 = $110).
4. Compound Percentage Changes: This involves applying multiple percentage changes sequentially. For example, "A price increased by 10% and then decreased by 5%. What is the final price?" This requires applying each percentage change one after another.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice solving percentage problems, the more comfortable and efficient you will become.
-
Understand the Fundamentals: A strong grasp of fractions and decimals is essential for mastering percentages.
-
Use Different Methods: Experiment with different methods (proportions, decimal conversion, calculator) to find the approach that suits you best.
-
Break Down Complex Problems: Large or complex problems can often be broken down into smaller, more manageable steps.
-
Check Your Answers: Always double-check your calculations to ensure accuracy.
-
Utilize Online Resources: Many websites and educational platforms offer practice problems and tutorials on percentage calculations.
Conclusion: The Power of Percentages
The ability to calculate percentages is an invaluable skill with a wide range of applications. From navigating daily finances to understanding complex statistical data, mastering percentage calculations empowers you to analyze information effectively and make informed decisions. By understanding the different methods and practicing regularly, you can confidently tackle various percentage problems and unlock the power of this fundamental mathematical concept. Remember, the core principle remains consistent: a percentage represents a part of a whole, expressed as a fraction of 100. With practice and a solid understanding of the underlying concepts, you’ll find percentage calculations to be straightforward and incredibly useful.
Latest Posts
Latest Posts
-
80 Kilos Cuanto Es En Libras
May 12, 2025
-
What Is The Greatest Common Factor Of 10 And 18
May 12, 2025
-
How Much Is 1 Yd Of Sand
May 12, 2025
-
120 Days From May 2 2024
May 12, 2025
-
Cuantos Anos Tienen Los Del 2006 En El 2024
May 12, 2025
Related Post
Thank you for visiting our website which covers about 0.2 Is What Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.