0.6 Is 10 Times As Much As
Treneri
May 10, 2025 · 4 min read
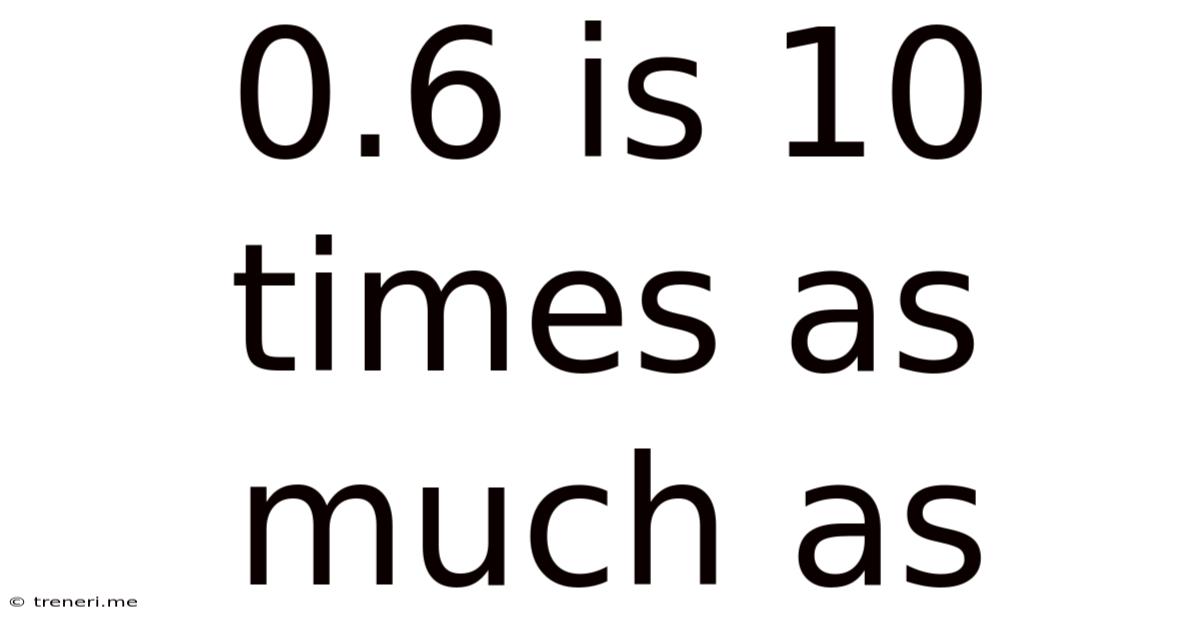
Table of Contents
0.6 is 10 Times as Much as: Exploring Decimal Relationships and Multiplication
Understanding decimal relationships is crucial for mastering fundamental math concepts. This article delves deep into the statement "0.6 is 10 times as much as," exploring its meaning, demonstrating its truth through various methods, and extending the concept to broader applications in mathematics and real-world scenarios. We'll unravel the mystery behind decimal multiplication and division, solidifying your understanding of these crucial arithmetic operations.
Understanding the Core Concept
The statement "0.6 is 10 times as much as" implies a multiplicative relationship between two decimal numbers. It means that if we take a certain number and multiply it by 10, the result will be 0.6. To find that number, we need to perform the inverse operation – division. Specifically, we need to divide 0.6 by 10.
Finding the Base Number
Let's represent the unknown number as 'x'. The problem can be expressed as an equation:
10x = 0.6
To solve for 'x', we divide both sides of the equation by 10:
x = 0.6 / 10
Performing the division, we get:
x = 0.06
Therefore, 0.6 is 10 times as much as 0.06.
Demonstrating the Relationship Through Different Methods
We can demonstrate this relationship using several approaches, solidifying our understanding and building a strong mathematical foundation.
Method 1: Using Fraction Equivalents
Decimals can be easily converted to fractions. Let's convert 0.6 and 0.06 to fractions:
- 0.6 = 6/10
- 0.06 = 6/100
Now, let's see if multiplying 6/100 by 10 gives us 6/10:
(6/100) * 10 = (6 * 10) / 100 = 60/100
Simplifying the fraction 60/100 by dividing both the numerator and the denominator by 20, we get:
60/100 = 6/10 = 0.6
This confirms that 0.6 is indeed 10 times as much as 0.06.
Method 2: Visual Representation using Decimal Models
Imagine a grid representing one whole unit, divided into 100 equal squares. 0.6 represents 60 of these squares (6/10 of the whole). 0.06 represents only 6 of these squares (6/100 of the whole). Visually, it's clear that 0.6 is significantly larger than 0.06; in fact, it's ten times bigger. Each group of 10 squares in the 0.6 representation is equivalent to one square in the 0.06 representation.
Method 3: Place Value Understanding
Understanding place value is key to grasping decimal operations. In the number 0.6, the '6' is in the tenths place. In the number 0.06, the '6' is in the hundredths place. Moving a digit one place to the left in a decimal number multiplies its value by 10. Therefore, moving the '6' from the hundredths place to the tenths place (as in 0.6) increases its value tenfold.
Extending the Concept: Multiplication and Division by Powers of 10
This example demonstrates a broader principle involving multiplying and dividing decimals by powers of 10 (10, 100, 1000, etc.). When multiplying a decimal by a power of 10, the decimal point moves to the right. When dividing, it moves to the left. The number of places the decimal point moves is equal to the number of zeros in the power of 10.
Multiplication Examples:
- 0.06 x 10 = 0.6 (Decimal point moves one place to the right)
- 0.06 x 100 = 6 (Decimal point moves two places to the right)
- 0.06 x 1000 = 60 (Decimal point moves three places to the right)
Division Examples:
- 0.6 / 10 = 0.06 (Decimal point moves one place to the left)
- 6 / 10 = 0.6 (Decimal point moves one place to the left)
- 60 / 100 = 0.6 (Decimal point moves two places to the left)
Real-World Applications
Understanding decimal relationships has numerous real-world applications:
- Finance: Calculating interest, discounts, tax rates, and currency conversions often involve decimal multiplication and division. For example, calculating 10% of a price involves multiplying the price by 0.1.
- Measurement: Many measurements use decimals, such as lengths (0.6 meters), weights (0.06 kilograms), and volumes (0.6 liters). Converting between units of measurement frequently uses multiplication and division by powers of 10.
- Science: Scientific calculations often involve decimal numbers representing very small or very large quantities.
- Engineering: Precision engineering relies heavily on accurate decimal calculations.
Practical Exercises to Strengthen Understanding
To solidify your understanding of the concepts discussed, try these exercises:
- Find the missing number: ? is 10 times as much as 0.008.
- Calculate: 0.35 x 100 = ?
- Solve: 7.2 / 1000 = ?
- Convert: Express 0.004 as a fraction.
- Real-world problem: A shirt costs $25. A discount of 0.1 (10%) is applied. Calculate the discount amount.
Conclusion: Mastering Decimal Relationships
Understanding the relationship between decimals, particularly the concept that 0.6 is 10 times as much as 0.06, is fundamental to mathematical proficiency. Through various methods of demonstration, from fractional equivalents to visual representations and place value analysis, we have explored this relationship in depth. By mastering decimal multiplication and division, especially involving powers of 10, you will be well-equipped to tackle a wide range of mathematical problems and real-world applications. The exercises provided offer opportunities to practice and reinforce your newly acquired knowledge, further enhancing your understanding of these crucial mathematical concepts. Remember, consistent practice is key to mastering any mathematical skill. Keep exploring, keep practicing, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
What Is Half A Hexagon Called
May 10, 2025
-
90 Days From June 28th 2024
May 10, 2025
-
92 Rounded To The Nearest Ten
May 10, 2025
-
How Many Grams Is 0 25 Oz
May 10, 2025
-
Cuanto Falta Para 24 De Septiembre
May 10, 2025
Related Post
Thank you for visiting our website which covers about 0.6 Is 10 Times As Much As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.