.01 To The Power Of 30
Treneri
May 10, 2025 · 5 min read
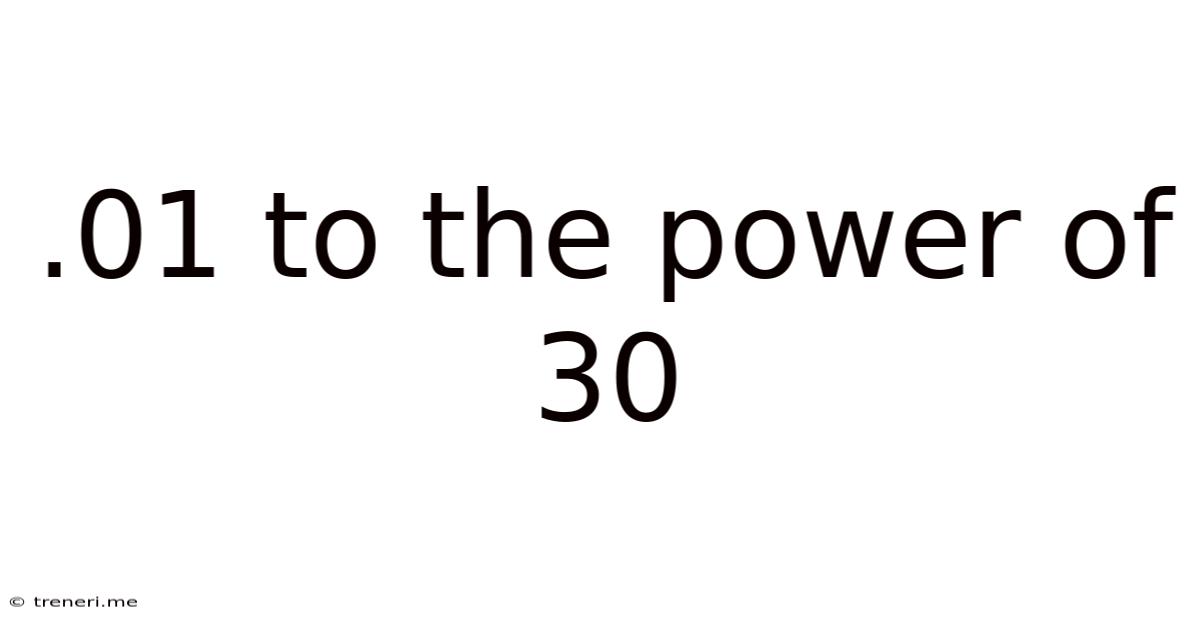
Table of Contents
.01 to the Power of 30: Unraveling the Mysteries of Exponents and Scientific Notation
Understanding exponents, particularly when dealing with decimal numbers raised to significant powers, can seem daunting. This article delves deep into the calculation and implications of 0.01 raised to the power of 30 (0.01<sup>30</sup>), exploring the underlying mathematical principles and its relevance in various fields. We'll uncover the surprising result and explore how to approach similar problems, equipping you with the tools to confidently tackle exponential calculations.
Understanding Exponents and Scientific Notation
Before we dive into the specific calculation of 0.01<sup>30</sup>, let's solidify our understanding of exponents and scientific notation. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example, 2<sup>3</sup> means 2 multiplied by itself three times (2 x 2 x 2 = 8).
Scientific notation is a crucial tool for expressing extremely large or extremely small numbers concisely. It represents a number in the form of a coefficient multiplied by 10 raised to a certain exponent. For instance, 1,000,000 can be written in scientific notation as 1 x 10<sup>6</sup>, and 0.000001 as 1 x 10<sup>-6</sup>.
Calculating 0.01 to the Power of 30
Now, let's tackle the core of this article: calculating 0.01<sup>30</sup>. We can approach this problem in a few ways. The most straightforward method involves recognizing that 0.01 is equivalent to 10<sup>-2</sup>. Therefore, our calculation becomes:
(10<sup>-2</sup>)<sup>30</sup>
Remember the rule of exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>m*n</sup>. Applying this rule, we get:
10<sup>(-2 * 30)</sup> = 10<sup>-60</sup>
This result, 10<sup>-60</sup>, is expressed in scientific notation. To convert it to a standard decimal form, we move the decimal point 60 places to the left. This results in a number with 59 zeros before the 1:
0.00000000000000000000000000000000000000000000000000000000000001
This incredibly small number highlights the rapid decrease in value when a number less than 1 is raised to a large power.
Practical Applications and Real-World Examples
While a number like 10<sup>-60</sup> might seem abstract and insignificant, its conceptual understanding has significant implications in various fields:
1. Physics and Nanotechnology:
In the realm of physics and nanotechnology, dealing with incredibly small quantities is commonplace. Concepts like the size of atoms, the wavelength of certain radiation, or the probability of certain quantum events often involve numbers of similar magnitude. Understanding exponential notation is crucial for representing and manipulating these quantities effectively.
2. Probability and Statistics:
Probability calculations often involve dealing with very small probabilities that, when raised to a power representing multiple independent events, result in extremely small overall probabilities. Consider the probability of a specific sequence of events occurring in a complex system – the result could easily be on the scale of 10<sup>-60</sup> or even smaller.
3. Computer Science and Data Storage:
In computer science, especially when dealing with large datasets or complex algorithms, understanding exponential growth (or decay) is vital. The time complexity of some algorithms can be described using exponential functions. Similarly, the probability of certain data errors or the chance of a specific event happening within a large system can be modeled with very small probabilities.
4. Financial Modeling:
Exponential functions are widely used in financial modeling, especially when dealing with compound interest or the growth of investments over very long time horizons. Although unlikely to encounter 10<sup>-60</sup> directly, the understanding of exponential decay applied to factors like depreciation or risk modeling is essential.
Exploring Variations and Related Calculations
Let's consider variations on the original calculation and explore similar problems to solidify your understanding of exponential calculations:
-
0.1<sup>30</sup>: This calculation would yield 10<sup>-30</sup>, a significantly larger number compared to 10<sup>-60</sup>, highlighting the importance of the base value in exponential calculations.
-
(0.01)<sup>x</sup>: Exploring different values of 'x' allows you to see the trend of exponential decay more clearly. Plotting the results on a graph would demonstrate the exponential nature of the decrease.
-
(0.001)<sup>30</sup>: This example would result in an even smaller number, illustrating how a smaller base value intensifies the effect of exponentiation.
-
Calculating the inverse: Understanding the inverse of 0.01<sup>30</sup> (i.e., 1/0.01<sup>30</sup> or 10<sup>60</sup>) provides insight into extremely large numbers and the symmetry between incredibly small and incredibly large quantities in the context of exponents and scientific notation.
The Importance of Precision and Significant Figures
When dealing with extremely small or large numbers, the concept of significant figures becomes crucial. In the context of 10<sup>-60</sup>, the only significant figure is the 1. All the trailing zeros are simply placeholders indicating the magnitude of the number. This highlights the limitations of representing such extremely small values in standard decimal form. Scientific notation offers a far more effective and precise way to represent them.
Conclusion: Mastering Exponents for a Deeper Understanding of the World
This article has explored the calculation and implications of 0.01 raised to the power of 30. We've seen that the result is an incredibly small number (10<sup>-60</sup>), which showcases the power of exponential decay and the importance of using scientific notation to represent such quantities. Understanding exponents and scientific notation isn't just a mathematical exercise; it's a fundamental skill applicable across various scientific and technical fields. By mastering these concepts, you'll gain a deeper appreciation of the vast scale of quantities in the universe and improve your ability to approach complex problems involving exponents. The exploration of variations and related calculations further strengthens this understanding and prepares you to tackle similar exponential problems with confidence. Remember, precision and the use of significant figures are vital when dealing with numbers of such magnitude.
Latest Posts
Latest Posts
-
How Many Days Since January 12 2023
May 10, 2025
-
De 12 A 8 Cuantas Horas Son
May 10, 2025
-
51 Rounded To The Nearest Hundred
May 10, 2025
-
1 Cup Of Pasta In Grams
May 10, 2025
-
How Long Is 109 Minutes In Hours
May 10, 2025
Related Post
Thank you for visiting our website which covers about .01 To The Power Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.