1/12 Of 1/3 Is What Fraction
Treneri
May 10, 2025 · 5 min read
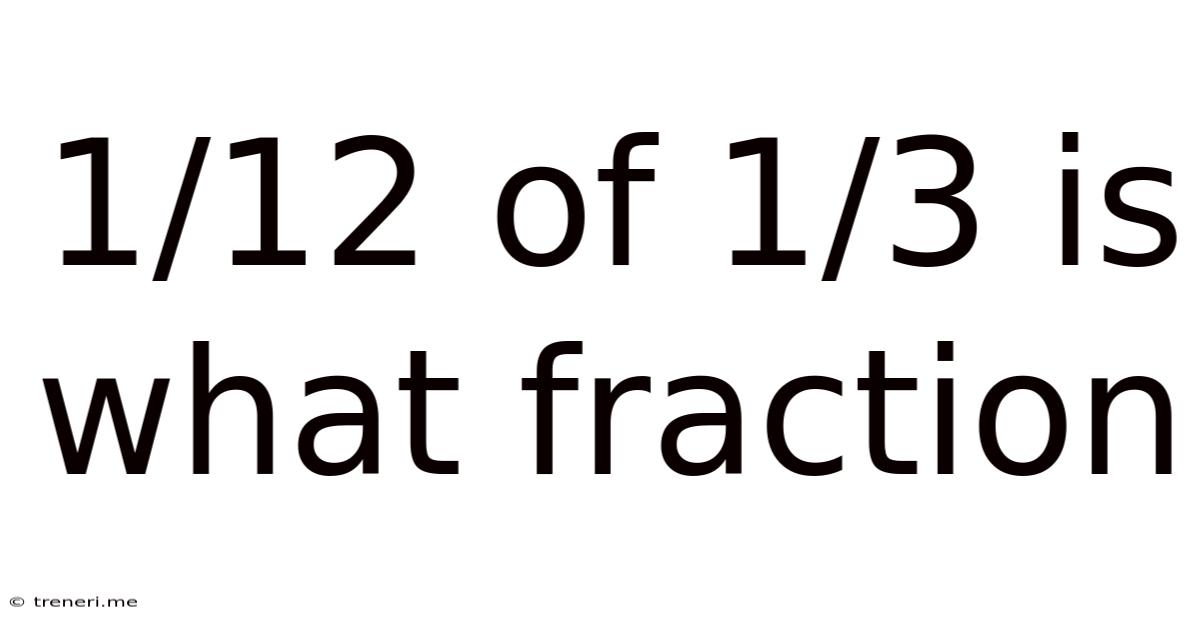
Table of Contents
1/12 of 1/3 is What Fraction? A Deep Dive into Fraction Multiplication
Understanding fractions is fundamental to mathematics, and mastering operations with them is crucial for success in various fields. This article will delve into the seemingly simple question, "1/12 of 1/3 is what fraction?", providing a comprehensive explanation that goes beyond the immediate answer. We'll explore the concept of fraction multiplication, offer multiple approaches to solving this problem, and discuss practical applications to solidify your understanding.
Understanding the Concept: "Of" Means Multiplication
The word "of" in mathematical terms, especially when dealing with fractions, signifies multiplication. Therefore, the question "1/12 of 1/3 is what fraction?" is essentially asking us to calculate (1/12) * (1/3).
Why is "Of" Multiplication?
Think of "of" as representing a portion or a part of a whole. If you have 1/2 of a pizza, it means you have half of the entire pizza. This "half of" translates directly to (1/2) * (whole pizza). The same principle applies to any fraction.
Method 1: Direct Multiplication of Fractions
The most straightforward method to solve (1/12) * (1/3) involves multiplying the numerators (top numbers) together and the denominators (bottom numbers) together:
(1/12) * (1/3) = (1 * 1) / (12 * 3) = 1/36
Therefore, 1/12 of 1/3 is 1/36.
Visualizing the Multiplication
Imagine a rectangular pizza divided into 12 equal slices. 1/12 represents one of these slices. Now, imagine dividing each of those 12 slices into 3 equal parts. This gives us a total of 12 * 3 = 36 smaller slices. 1/12 of 1/3 represents one of these 36 smaller slices.
Method 2: Simplifying Before Multiplication (Optional)
While direct multiplication is efficient, sometimes simplifying fractions before multiplying can make the calculation easier. In this case, there are no common factors between the numerators and denominators that we can simplify before multiplying. However, let's illustrate this method with a different example.
Let's say we want to find 2/6 of 3/9.
- Simplify the fractions: 2/6 simplifies to 1/3 and 3/9 simplifies to 1/3.
- Multiply the simplified fractions: (1/3) * (1/3) = 1/9
This demonstrates how simplifying before multiplying can lead to smaller numbers and easier calculations.
Method 3: Using the Concept of "Parts of Parts"
This method is particularly useful for visualizing the problem and understanding the underlying logic.
Imagine you have a whole object divided into 3 equal parts. Each part represents 1/3 of the whole. Now, take one of these parts (1/3) and divide it into 12 equal smaller parts. Each of these smaller parts is (1/3) / 12 = 1/36 of the original whole. This reinforces the result we obtained through direct multiplication.
Applications of Fraction Multiplication
Understanding fraction multiplication has broad applications across various fields:
1. Baking and Cooking:
Recipes often require fractional measurements. For instance, if a recipe calls for 1/3 of a cup of sugar, and you want to make only 1/2 the recipe, you would need to calculate (1/2) * (1/3) = 1/6 of a cup of sugar.
2. Construction and Engineering:
In construction and engineering projects, precise measurements are critical. Calculations involving fractions are frequently used to determine the amount of materials required or the dimensions of components.
3. Finance and Economics:
Fraction multiplication is essential for calculating proportions, percentages, and interest rates. For example, if an investment grows by 1/4 of its value, and the initial value was 1/2 of a total amount, the increase would be calculated using fraction multiplication.
4. Science and Data Analysis:
Scientific experiments and data analysis often involve dealing with fractions and ratios. Understanding fraction operations is crucial for accurately interpreting and presenting results.
Expanding on Fraction Operations: Addition, Subtraction, and Division
While this article focuses on multiplication, it’s important to briefly touch upon other fraction operations to provide a more holistic understanding.
Addition and Subtraction of Fractions:
To add or subtract fractions, they must have the same denominator (bottom number). If they don't, find the least common denominator (LCD) and convert the fractions accordingly. Then, add or subtract the numerators, keeping the denominator the same.
For example: 1/4 + 1/2 = 1/4 + 2/4 = 3/4
Division of Fractions:
Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by flipping the numerator and denominator.
For example: (1/2) / (1/3) = (1/2) * (3/1) = 3/2
Mastering Fractions: Practice and Resources
The key to mastering fractions is consistent practice. Work through various problems, including those involving different operations. You can find many online resources and workbooks offering practice exercises. Focus on understanding the underlying principles rather than just memorizing formulas.
Conclusion: The Power of Fractional Understanding
Understanding fractions, and specifically, multiplication of fractions, is a critical mathematical skill with far-reaching applications. The seemingly simple problem of calculating "1/12 of 1/3" serves as a gateway to a deeper understanding of this fundamental concept. By mastering these operations, you'll enhance your problem-solving abilities across numerous disciplines and gain a valuable tool for navigating the world of numbers. Remember that consistent practice and a focus on the underlying principles are key to achieving true proficiency. So, grab a pencil and paper and start practicing! The world of fractions awaits!
Latest Posts
Latest Posts
-
How Many Pounds Of Mashed Potatoes For 100
May 11, 2025
-
How To Find Frequency Of Pendulum
May 11, 2025
-
How Many Minutes Is 140 Seconds
May 11, 2025
-
Circumference Of A Circle Divided By Its Diameter
May 11, 2025
-
1100 Watt To 700 Watt Microwave Conversion
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1/12 Of 1/3 Is What Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.