1/2 + 3/8 In Fraction Form
Treneri
May 11, 2025 · 6 min read
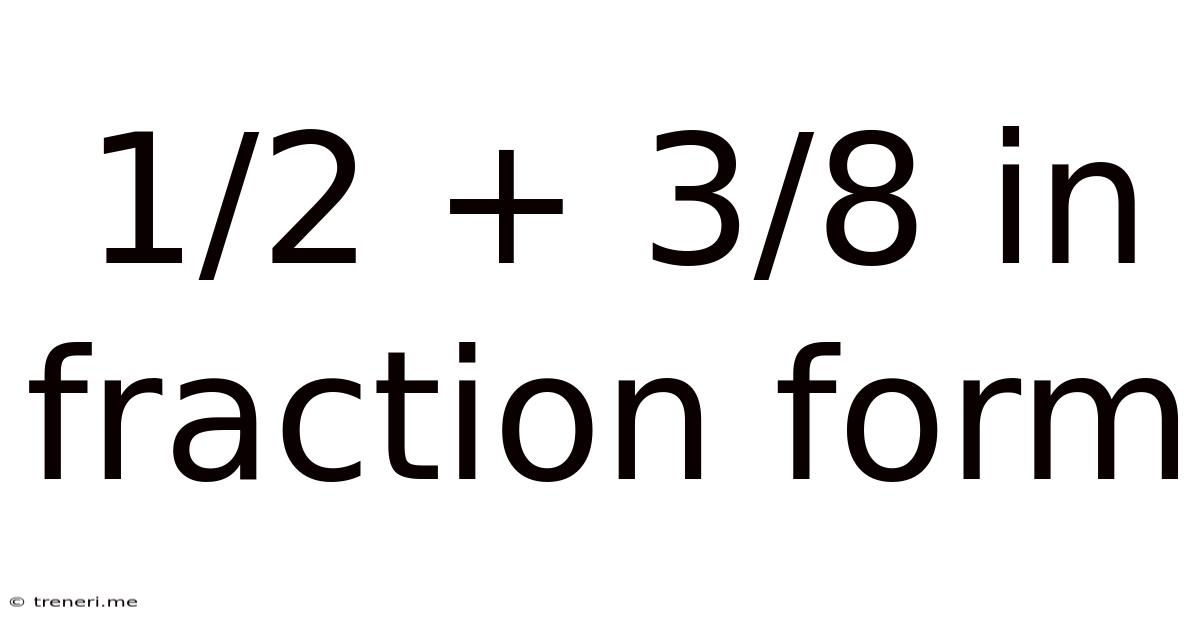
Table of Contents
1/2 + 3/8: A Deep Dive into Fraction Addition
Adding fractions might seem like a simple arithmetic task, but mastering it forms the foundation for more complex mathematical concepts. This comprehensive guide will explore the addition of 1/2 and 3/8, breaking down the process step-by-step and delving into the underlying principles. We'll also explore various methods, practical applications, and even touch upon the historical context of fractions.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's review the fundamental components of a fraction:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
In the fraction 1/2, 1 is the numerator (one part) and 2 is the denominator (two equal parts making a whole). Similarly, in 3/8, 3 is the numerator and 8 is the denominator.
Why We Need a Common Denominator
The core principle of adding fractions is that we can only directly add numerators when the denominators are the same. Think of it like adding apples and oranges – you can't directly combine them until you have a common unit of measurement. In fractions, this common unit is the denominator.
In our problem, 1/2 + 3/8, the denominators are 2 and 8. They are not the same, so we need to find a common denominator.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that both 2 and 8 divide into evenly. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find a common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12...
- Multiples of 8: 8, 16, 24... The least common multiple is 8.
-
Prime Factorization: Break down each denominator into its prime factors.
- 2 = 2
- 8 = 2 x 2 x 2 = 2³ The LCD is the product of the highest powers of all the prime factors present: 2³ = 8.
In both cases, the LCD is 8.
Converting Fractions to the Common Denominator
Now that we have the LCD (8), we need to convert both fractions so they have a denominator of 8.
-
Converting 1/2: To change the denominator from 2 to 8, we multiply both the numerator and the denominator by 4 (because 2 x 4 = 8): (1 x 4) / (2 x 4) = 4/8
-
Converting 3/8: This fraction already has a denominator of 8, so it remains unchanged: 3/8
Performing the Addition
Now that both fractions have the same denominator, we can add them:
4/8 + 3/8 = (4 + 3) / 8 = 7/8
Therefore, 1/2 + 3/8 = 7/8
Simplifying Fractions (If Necessary)
Sometimes, after adding fractions, the result can be simplified. A fraction is simplified when the greatest common divisor (GCD) of the numerator and denominator is 1. In our case, 7/8 is already in its simplest form because 7 and 8 have no common divisors other than 1.
Visualizing Fraction Addition
Visual representations can greatly aid understanding. Imagine a circle divided into eight equal parts. 1/2 represents four of these parts (4/8), and 3/8 represents three parts. Adding them together gives you seven parts out of eight (7/8).
Real-World Applications of Fraction Addition
Adding fractions isn't just an abstract mathematical exercise; it has numerous practical applications in everyday life:
- Cooking and Baking: Following recipes often requires adding fractional amounts of ingredients.
- Measurement: Measuring lengths, volumes, or weights frequently involves fractions.
- Construction and Engineering: Precise measurements are crucial, and fractions are essential for accurate calculations.
- Finance: Dealing with portions of money or shares often involves fractional calculations.
Different Methods for Adding Fractions
While the common denominator method is the most widely used, alternative approaches exist:
-
Using Decimals: Convert the fractions to decimals (1/2 = 0.5, 3/8 = 0.375), add them (0.5 + 0.375 = 0.875), and then convert the decimal back to a fraction (0.875 = 7/8). This method is useful when dealing with fractions that are easily converted to decimals.
-
Finding a Common Multiple (Not Necessarily the LCD): While using the LCD simplifies the process, you can also add fractions using any common multiple. For example, you could use 16 as the common denominator, resulting in 8/16 + 6/16 = 14/16. This fraction simplifies to 7/8. However, using the LCD always keeps the numbers smaller and makes simplification easier.
Historical Context of Fractions
Fractions have a rich history, appearing in various ancient civilizations. The Egyptians, for instance, used unit fractions (fractions with a numerator of 1) extensively. Babylonian mathematics used a sexagesimal system (base 60), which influenced our modern-day use of minutes and seconds. The development of modern fractional notation took centuries, with various notations used before the familiar numerator/denominator form became standard.
Troubleshooting Common Mistakes in Fraction Addition
Several common mistakes can occur when adding fractions:
-
Forgetting the Common Denominator: This is the most frequent error. Always ensure both fractions have the same denominator before adding the numerators.
-
Incorrectly Finding the LCD: Carefully determine the least common denominator. Using a larger common multiple is acceptable but can lead to more complex simplification.
-
Adding Denominators: Remember that you only add the numerators; the denominator remains the same.
-
Not Simplifying the Result: Always simplify the final fraction to its lowest terms.
Advanced Fraction Operations: Building Upon the Basics
Mastering the addition of fractions like 1/2 + 3/8 is crucial because it forms the basis for more complex operations involving fractions:
-
Subtraction of Fractions: The process is very similar to addition, requiring a common denominator before subtracting the numerators.
-
Multiplication of Fractions: Multiply the numerators together and the denominators together. Simplification is often possible before or after multiplication.
-
Division of Fractions: Invert the second fraction (reciprocal) and then multiply.
-
Mixed Numbers: Mixed numbers (a whole number and a fraction, like 1 1/2) require converting them into improper fractions before performing addition, subtraction, multiplication, or division.
Conclusion: Mastering Fraction Addition
Adding fractions, such as 1/2 + 3/8, might appear daunting at first, but with a methodical approach and a solid understanding of the underlying principles, it becomes a manageable and essential skill. By mastering the common denominator method and understanding the reasons behind each step, you'll not only solve this particular problem but gain the confidence to tackle more complex fraction problems, enhancing your mathematical abilities and preparedness for real-world scenarios. Remember to practice regularly and visualize the process whenever possible to solidify your understanding and achieve mastery. The journey from understanding basic fractions to tackling advanced operations opens doors to a world of mathematical exploration and application.
Latest Posts
Latest Posts
-
What Is The Equivalent Fraction Of 9 12
May 12, 2025
-
How Many Hours Are In Seven Days
May 12, 2025
-
Cuanto Es 18 Oz En Litros
May 12, 2025
-
How Many Miles Is 49 Km
May 12, 2025
-
Time And A Half For 22 An Hour
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 3/8 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.