1 2 Divided By 2 3 In Fraction Form
Treneri
May 10, 2025 · 5 min read
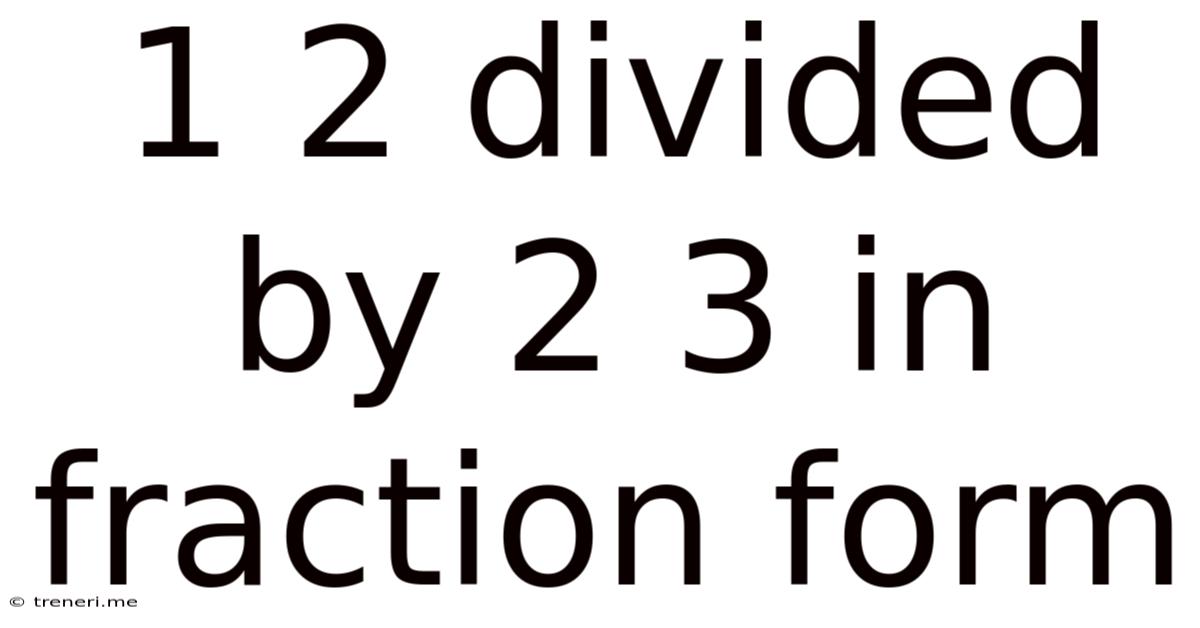
Table of Contents
1 2/3 Divided by 2: A Comprehensive Guide to Fraction Division
The seemingly simple problem of dividing mixed numbers can often present a challenge, particularly when dealing with fractions. Let's delve into the process of solving 1 2/3 divided by 2, not just finding the answer, but understanding the underlying principles of fraction division and developing a robust method applicable to a wide range of similar problems. This guide will cover the steps, provide alternative approaches, and explore related concepts to solidify your understanding.
Understanding Mixed Numbers and Fractions
Before tackling the division, it's crucial to understand the components involved. A mixed number, like 1 2/3, combines a whole number (1) and a proper fraction (2/3). This represents 1 + 2/3. To perform calculations effectively, it's often easier to convert mixed numbers into improper fractions.
An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). To convert 1 2/3 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 3 = 3
- Add the numerator: 3 + 2 = 5
- Keep the same denominator: 5/3
Therefore, 1 2/3 is equivalent to 5/3.
Dividing Fractions: The Reciprocal Method
The most common and efficient method for dividing fractions involves using reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 2 (which can be written as 2/1) is 1/2.
The process of dividing fractions then becomes a process of multiplication:
-
Convert any mixed numbers to improper fractions. As we've established, 1 2/3 becomes 5/3. The number 2 can be written as 2/1.
-
Replace the division sign with a multiplication sign and use the reciprocal of the second fraction. This is the key step. Our problem changes from (5/3) ÷ (2/1) to (5/3) x (1/2).
-
Multiply the numerators together and the denominators together. This gives us (5 x 1) / (3 x 2) = 5/6.
Therefore, 1 2/3 divided by 2 equals 5/6.
Visualizing Fraction Division
Understanding fraction division visually can be helpful. Imagine you have a pizza cut into three slices. 1 2/3 pizzas would represent five of these slices (1 whole pizza plus 2/3 of another). If you want to divide these five slices equally among two people, each person gets 5/6 of a pizza. This visual representation reinforces the result we obtained mathematically.
Alternative Methods: Using Decimal Conversions
While the reciprocal method is generally preferred for its efficiency and clarity, you can also solve this problem by converting the mixed number into a decimal and then performing the division.
-
Convert the mixed number to a decimal: 1 2/3 is equal to 1.666... (or approximately 1.67).
-
Perform the decimal division: 1.666... ÷ 2 ≈ 0.833...
-
Convert the decimal back to a fraction (if needed): 0.833... is approximately 5/6. Note that due to the repeating decimal, the decimal conversion method may introduce a small degree of error. The fraction method provides a more precise and exact answer.
Extending the Concept: More Complex Fraction Division Problems
The principles discussed here can be readily applied to more complex problems involving mixed numbers and fractions. For instance, let's consider a problem like (2 1/4) ÷ (3/5):
-
Convert mixed numbers to improper fractions: 2 1/4 becomes (2*4 + 1)/4 = 9/4
-
Use the reciprocal method: (9/4) ÷ (3/5) becomes (9/4) x (5/3)
-
Multiply: (9 x 5) / (4 x 3) = 45/12
-
Simplify the fraction: 45/12 can be simplified by dividing both the numerator and denominator by their greatest common divisor (3), resulting in 15/4.
This can be further converted to a mixed number: 15/4 = 3 3/4
Common Mistakes to Avoid
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before performing the division.
- Inverting the wrong fraction: Remember to take the reciprocal of the second fraction (the divisor) only.
- Incorrect multiplication: Pay close attention when multiplying numerators and denominators.
- Not simplifying the final fraction: Always simplify the resulting fraction to its lowest terms.
Practical Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in various fields:
- Cooking and baking: Scaling recipes up or down often involves dividing fractions.
- Sewing and tailoring: Calculating fabric needs for garments.
- Construction and carpentry: Dividing lumber or materials accurately.
- Engineering and design: Precise measurements and calculations.
- Financial calculations: Working with percentages and shares.
Conclusion: Mastering Fraction Division
Dividing fractions, especially mixed numbers, requires a systematic approach. By understanding the concepts of improper fractions, reciprocals, and the principles of fraction multiplication, you can confidently tackle a wide range of problems. Remember to break down complex problems into smaller, manageable steps, and double-check your work to ensure accuracy. Mastering fraction division equips you with a fundamental skill applicable to various aspects of daily life and professional endeavors. The detailed explanation and examples provided in this guide should empower you to approach future fraction division problems with increased confidence and precision. Practice is key to solidifying your understanding and building proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
6 Ounce Is How Many Cups
May 10, 2025
-
I Have 6 Valence Electrons And 16 Protons
May 10, 2025
-
Best Size Mirror For 48 Inch Vanity
May 10, 2025
-
How Much Is 3 Ml Of Water
May 10, 2025
-
Cuanto Falta Para El 21 De Noviembre
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 2 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.