1 2 Divided By 2 5
Treneri
May 10, 2025 · 5 min read
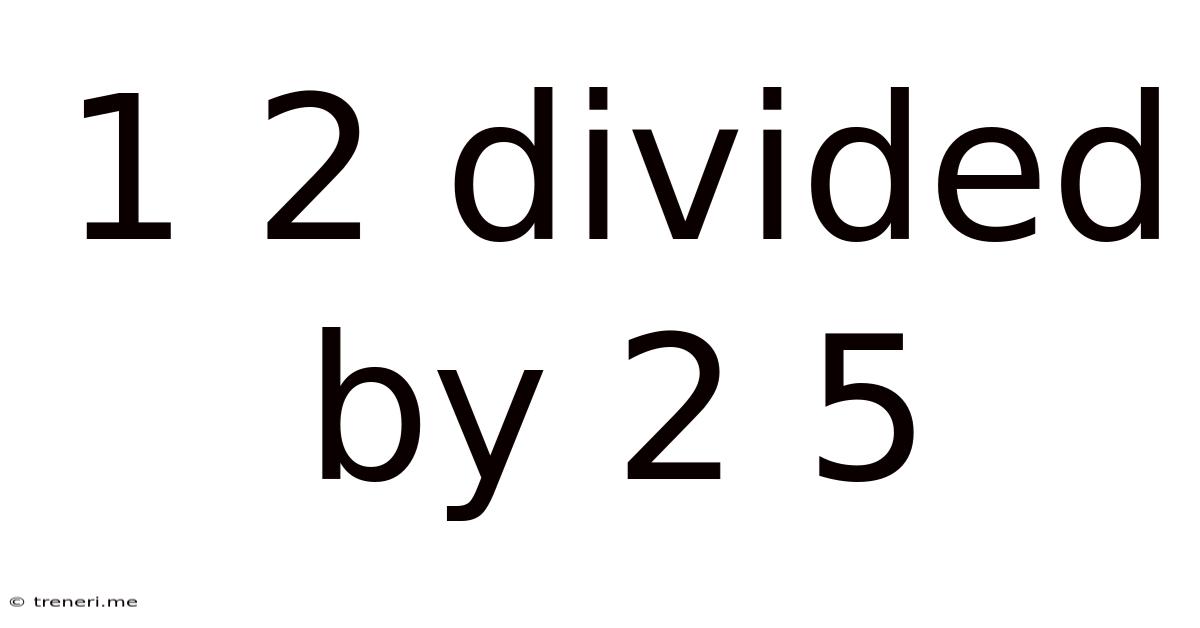
Table of Contents
12 Divided by 25: A Deep Dive into Mathematical Concepts and Real-World Applications
The seemingly simple mathematical expression "12 divided by 25" offers a fascinating opportunity to explore several key mathematical concepts and their applications in various fields. While the immediate answer, obtained through simple division, might seem straightforward, a deeper analysis reveals the richness and versatility of this seemingly basic operation. This article will explore various methods of solving this division problem, discuss the underlying mathematical principles, and illustrate its practical relevance in everyday life and specialized domains.
Understanding Division: A Fundamental Arithmetic Operation
Division, one of the four fundamental arithmetic operations (along with addition, subtraction, and multiplication), is essentially the process of splitting a quantity into equal parts. In the expression "12 divided by 25," 12 represents the dividend (the quantity being divided), and 25 is the divisor (the quantity by which we are dividing). The result, often called the quotient, represents the number of times the divisor goes into the dividend. In this case, since 12 is smaller than 25, the quotient will be a fraction or decimal less than 1.
Different Approaches to Solving 12 Divided by 25
There are several ways to calculate 12 divided by 25:
-
Long Division: This traditional method involves systematically dividing the dividend by the divisor, resulting in a quotient and potentially a remainder. While effective, it can be somewhat time-consuming, especially with larger numbers. In this instance, long division would yield 0 with a remainder of 12, implying the quotient is a fraction.
-
Fraction Conversion: The expression "12 divided by 25" can be directly represented as a fraction: 12/25. This fraction is already in its simplest form, as 12 and 25 share no common factors other than 1. This fractional representation is often preferred for its clarity and precision.
-
Decimal Conversion: To obtain a decimal representation, we can simply perform the division using a calculator or long division. 12 divided by 25 equals 0.48. This decimal form is useful for practical applications where fractional representations are less convenient.
-
Percentage Conversion: The decimal 0.48 can also be expressed as a percentage by multiplying by 100. Therefore, 12 divided by 25 is equivalent to 48%. This percentage representation is widely used to express proportions and ratios.
Mathematical Concepts Illuminated
The seemingly simple problem of dividing 12 by 25 touches upon several important mathematical ideas:
Fractions and Decimals: Interchangeability and Equivalence
The ability to seamlessly convert between fractions and decimals highlights the fundamental relationship between these two representations of numbers. Fractions provide an exact representation, while decimals can offer practical approximations, depending on the level of precision required. The equivalence between 12/25 and 0.48 demonstrates this interchangeability effectively.
Ratios and Proportions: Understanding Relationships
The expression can also be viewed as a ratio, expressing the relationship between 12 and 25. This ratio can be used to solve various proportion problems. For example, if 12 represents a part of a whole, and 25 represents the whole, we can use this ratio to find other proportional parts.
Remainders and Modular Arithmetic: Exploring Beyond the Quotient
In long division, the remainder (12 in this case) highlights the concept of modular arithmetic. Modular arithmetic deals with remainders after division, finding applications in cryptography, computer science, and other fields.
Real-World Applications: Beyond the Textbook
The seemingly simple calculation of "12 divided by 25" has practical applications across many disciplines:
Everyday Life: Budgeting, Cooking, and More
-
Budgeting: Imagine you have $12 and want to allocate it equally among 25 small expenses. Dividing 12 by 25 helps determine how much you can spend on each expense (approximately $0.48).
-
Cooking: If a recipe calls for 25 units of an ingredient, but you only have 12, you can use the calculation to determine the proportional amount to use to adapt the recipe.
-
Sharing Resources: Imagine sharing 12 toys among 25 children. The calculation helps in understanding the proportion each child receives.
Specialized Fields: Engineering, Finance, and Science
-
Engineering: In engineering design, ratios and proportions are critical. Calculating the relative strengths of materials or the scaling of models involves similar calculations.
-
Finance: Financial calculations often involve ratios and percentages. For example, calculating return on investment or expressing a portion of a budget often requires such calculations.
-
Science: Scientific data analysis frequently utilizes ratios and proportions. For instance, calculating concentrations of solutions or determining statistical probabilities involves similar mathematical concepts.
Advanced Concepts and Extensions
The problem of 12 divided by 25 can be used as a stepping stone to explore more advanced mathematical concepts:
Continued Fractions: Infinite Representations
The fraction 12/25 can be expressed as a continued fraction, a unique representation as an infinite series of fractions. While this concept might seem abstract, it has applications in number theory and approximation theory.
Complex Numbers: Expanding the Number System
The principles of division extend beyond real numbers to complex numbers. While not directly applicable to 12/25, understanding the extension to complex numbers is crucial in advanced mathematics and physics.
Conclusion: The Power of Simplicity
The seemingly simple mathematical expression "12 divided by 25" unveils a wealth of mathematical concepts and practical applications. From fundamental arithmetic operations to advanced concepts, this simple calculation serves as a potent reminder of the interconnectedness of mathematical ideas and their widespread relevance in various aspects of life. By understanding the different methods of solving this problem and the principles behind them, we gain a deeper appreciation for the power and versatility of mathematics in both theoretical and applied contexts. This comprehensive exploration demonstrates the rich potential hidden within even the simplest of mathematical expressions, encouraging a deeper engagement with the beauty and utility of mathematics.
Latest Posts
Latest Posts
-
How Much Is 3 Ml Of Water
May 10, 2025
-
Cuanto Falta Para El 21 De Noviembre
May 10, 2025
-
What Is A 27 Out Of 31
May 10, 2025
-
How Is True Shooting Percentage Calculated
May 10, 2025
-
Can You Tan With A Uv Of 3
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.