1/2 X 1/3 As A Fraction
Treneri
May 10, 2025 · 5 min read
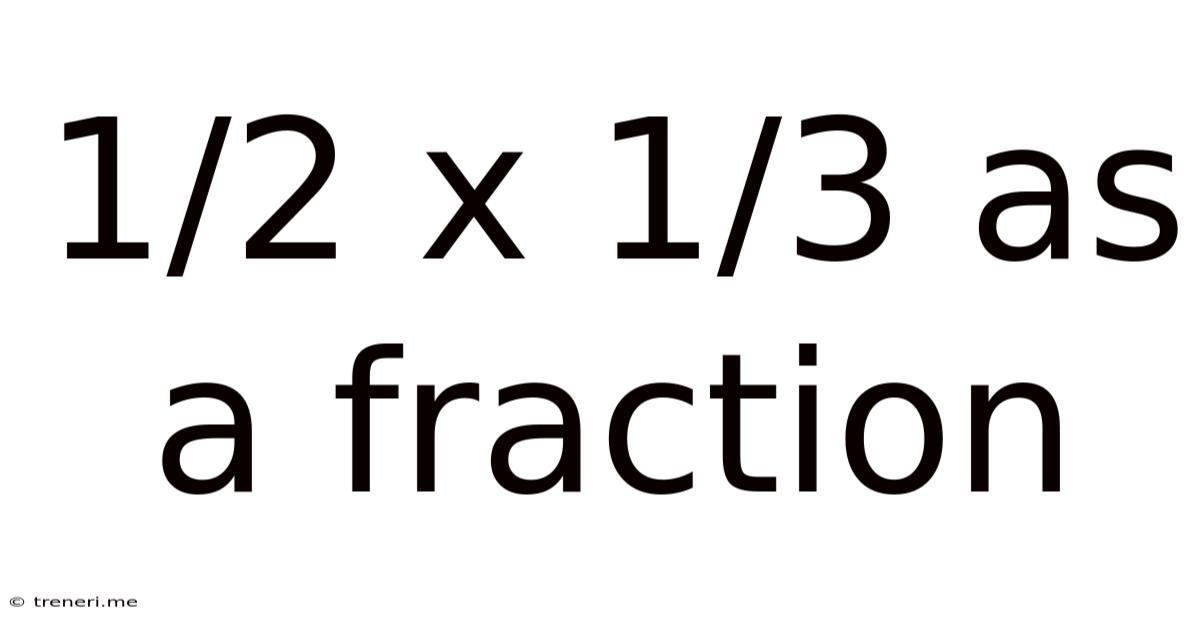
Table of Contents
1/2 x 1/3 as a Fraction: A Comprehensive Guide
Multiplying fractions might seem daunting at first, but with a clear understanding of the process, it becomes a straightforward task. This comprehensive guide delves into the multiplication of 1/2 and 1/3, explaining the method, providing visual aids, and exploring related concepts to solidify your understanding. We'll also discuss the broader context of fraction multiplication and its applications in various fields.
Understanding Fraction Multiplication
Before tackling the specific problem of 1/2 x 1/3, let's establish the fundamental principles of multiplying fractions. The core concept is simple: multiply the numerators (top numbers) together and multiply the denominators (bottom numbers) together.
This can be expressed as a general formula:
(a/b) x (c/d) = (a x c) / (b x d)
Where 'a', 'b', 'c', and 'd' represent any numbers, and 'b' and 'd' cannot be zero (division by zero is undefined).
This method works because fractions represent parts of a whole. When multiplying fractions, we are essentially finding a fraction of a fraction. For instance, 1/2 x 1/3 means finding one-third of one-half.
Solving 1/2 x 1/3
Now, let's apply this principle to our specific problem: 1/2 x 1/3.
Following the formula above:
1/2 x 1/3 = (1 x 1) / (2 x 3) = 1/6
Therefore, 1/2 multiplied by 1/3 equals 1/6.
Visual Representation
Visualizing the multiplication can enhance understanding. Imagine a rectangle divided into two equal halves (representing 1/2). Now, divide each of those halves into three equal parts (representing 1/3). You'll find that the entire rectangle is now divided into six equal parts. The area representing 1/2 x 1/3 is one of those six parts – hence, 1/6.
(Insert a visual here showing a rectangle divided into halves, then each half divided into thirds, highlighting one resulting sixth). While I can't create images directly, I strongly suggest you create this image yourself using a drawing tool or find a similar image online. This visual will greatly aid your comprehension.
Simplifying Fractions (If Necessary)
Sometimes, after multiplying fractions, the resulting fraction can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In our case, 1/6 is already in its simplest form, as 1 and 6 share no common divisors other than 1.
Let's consider another example:
1/2 x 2/4 = (1 x 2) / (2 x 4) = 2/8
Here, 2/8 can be simplified. The GCD of 2 and 8 is 2. Dividing both numerator and denominator by 2, we get:
2/8 = 1/4
Therefore, 1/2 x 2/4 simplifies to 1/4.
Applications of Fraction Multiplication
Fraction multiplication isn't confined to mathematical exercises; it finds practical applications in numerous real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'd multiply 1/2 cup by 1/2, resulting in 1/4 cup.
-
Measurement and Construction: In construction or engineering, precise measurements often involve fractions. Calculating areas or volumes frequently involves multiplying fractional values.
-
Finance and Budgeting: Portioning budgets or calculating percentages often relies on multiplying fractions. For example, if you want to allocate 1/3 of your monthly budget to savings, you would multiply your total budget by 1/3.
-
Probability and Statistics: The calculation of probabilities often involves multiplying fractions representing individual probabilities of events.
-
Data Analysis: In data analysis, especially working with proportions and percentages, you'll frequently encounter fraction multiplication.
Mixed Numbers and Fraction Multiplication
What if one or both of the numbers are mixed numbers (a whole number and a fraction)? You need to convert them to improper fractions before applying the multiplication rule.
An improper fraction has a numerator larger than or equal to its denominator.
For example: 1 1/2 x 2/3
First, convert 1 1/2 to an improper fraction:
1 1/2 = (1 x 2 + 1) / 2 = 3/2
Now, multiply the improper fractions:
3/2 x 2/3 = (3 x 2) / (2 x 3) = 6/6 = 1
Therefore, 1 1/2 x 2/3 = 1
Further Exploration: Reciprocal and Division
The concept of reciprocals is closely linked to fraction multiplication. The reciprocal of a fraction is obtained by swapping the numerator and denominator. For example, the reciprocal of 1/2 is 2/1 (or simply 2).
Division of fractions involves multiplying by the reciprocal of the second fraction:
a/b ÷ c/d = a/b x d/c
Conclusion: Mastering Fraction Multiplication
Understanding fraction multiplication is a fundamental skill with wide-ranging applications. By grasping the basic principle of multiplying numerators and denominators, and by practicing with various examples, including mixed numbers, you'll build confidence and proficiency in this essential mathematical operation. Remember to always simplify your answer to its lowest terms for a complete and accurate result. Use visual aids and real-world examples to reinforce your understanding and appreciate the practical relevance of this seemingly simple yet powerful mathematical tool. Through consistent practice and a deeper exploration of related concepts like reciprocals and fraction division, you will master the art of fraction multiplication and confidently apply it in various contexts.
Latest Posts
Latest Posts
-
26 Km Equals How Many Miles
May 11, 2025
-
How Much Is A 1 4 Pound Of Butter
May 11, 2025
-
Write The Slope Intercept Form Of The Equation For Each Line
May 11, 2025
-
What Uv Index Is Best To Tan
May 11, 2025
-
Least Common Multiple 2 And 9
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1/2 X 1/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.