1/3 Divided By 1/2 As A Fraction
Treneri
May 12, 2025 · 5 min read
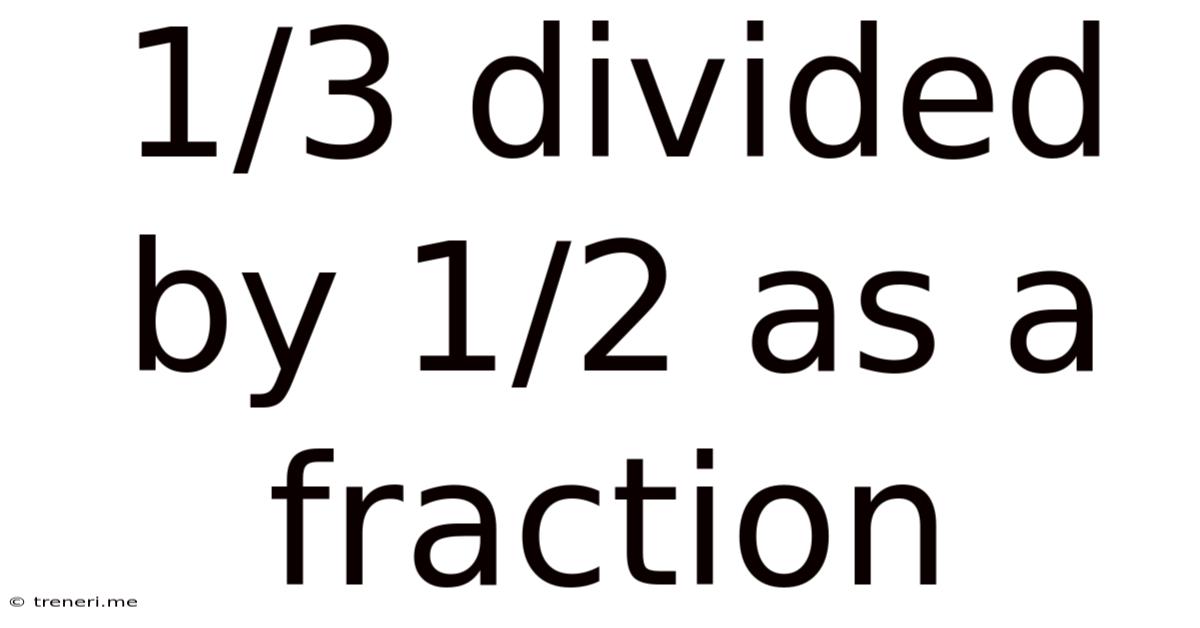
Table of Contents
1/3 Divided by 1/2 as a Fraction: A Comprehensive Guide
Understanding fractions and how to perform operations with them is a fundamental skill in mathematics. While seemingly simple, dividing fractions can sometimes be confusing. This comprehensive guide will walk you through the process of solving 1/3 divided by 1/2, explaining the underlying concepts and offering various approaches to arrive at the correct solution. We’ll also explore related concepts to solidify your understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem of 1/3 divided by 1/2, let's establish a solid foundation in fraction division. The core concept revolves around reciprocals and multiplication.
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/2 is 2/1 (or simply 2).
Therefore, the general rule for dividing fractions is:
a/b ÷ c/d = a/b × d/c
This means we flip the second fraction (the divisor) and multiply the two fractions together. This process simplifies the division into a more manageable multiplication problem.
Solving 1/3 Divided by 1/2
Now, let's apply this rule to our specific problem: 1/3 divided by 1/2.
Following the rule above:
1/3 ÷ 1/2 = 1/3 × 2/1
Now, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(1 × 2) / (3 × 1) = 2/3
Therefore, 1/3 divided by 1/2 equals 2/3.
Visualizing the Solution
Understanding fractions can be significantly easier when you visualize them. Imagine you have 1/3 of a pizza. Now, you want to divide that 1/3 into 1/2 portions. How many 1/2 portions do you have? The answer is 2/3 of a whole pizza. The process shows that dividing a smaller fraction by another fraction can lead to a larger result.
Alternative Methods and Explanations
While the reciprocal method is the most efficient, let's explore other ways to conceptualize this problem:
Method 1: Using Common Denominators
While less efficient for this specific problem, understanding this method is valuable for more complex scenarios. To divide fractions using common denominators:
- Find a common denominator: The common denominator for 3 and 2 is 6.
- Convert the fractions: 1/3 becomes 2/6 and 1/2 becomes 3/6.
- Divide the numerators: 2/6 ÷ 3/6 = 2 ÷ 3 = 2/3
This method highlights the underlying concept that dividing fractions involves comparing their relative sizes when expressed with a common denominator.
Method 2: Using Decimal Equivalents
You can also solve this problem by converting the fractions into decimals and then dividing.
1/3 ≈ 0.333… 1/2 = 0.5
0.333… ÷ 0.5 ≈ 0.666…
Converting 0.666… back to a fraction gives us approximately 2/3. This method is less precise with repeating decimals but provides an alternative perspective. It's crucial to remember that this approach might yield an approximate answer due to rounding errors associated with repeating decimals.
Expanding on Fraction Division Concepts
Understanding 1/3 divided by 1/2 lays the groundwork for tackling more complex fraction problems. Let’s explore some related concepts:
Dividing Fractions with Whole Numbers
When dividing a fraction by a whole number, remember that a whole number can be expressed as a fraction with a denominator of 1. For instance, dividing 1/3 by 2 is the same as 1/3 ÷ 2/1.
Following the rules of fraction division:
1/3 ÷ 2/1 = 1/3 × 1/2 = 1/6
Dividing Mixed Numbers
Mixed numbers combine whole numbers and fractions (e.g., 1 1/2). To divide mixed numbers, you first convert them into improper fractions (fractions where the numerator is greater than the denominator). Then, follow the standard fraction division procedure.
For example, to divide 1 1/2 by 1/3, we first convert 1 1/2 to 3/2.
3/2 ÷ 1/3 = 3/2 × 3/1 = 9/2 or 4 1/2
Dividing Fractions with Larger Numbers
The same principles apply when dividing fractions with larger numbers. The key is always to convert to improper fractions if needed, find the reciprocal of the divisor, and multiply.
For example: 12/5 ÷ 6/7 = 12/5 × 7/6 = (12 x 7) / (5 x 6) = 84/30 = 14/5 or 2 4/5
Practical Applications of Fraction Division
Understanding fraction division isn't merely an academic exercise. It has numerous real-world applications, including:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Construction and Carpentry: Precise measurements often involve fractions.
- Sewing and Tailoring: Calculating fabric requirements necessitates fraction manipulation.
- Finance: Calculating percentages and proportions in budgeting or investments.
- Science: Measuring and manipulating quantities in experiments.
Conclusion: Mastering Fraction Division
Mastering fraction division is essential for success in various mathematical and real-world contexts. While the concept might seem daunting at first, it simplifies to a straightforward process of multiplying by the reciprocal. By understanding the underlying principles, visualizing the problem, and practicing regularly, you can confidently tackle any fraction division challenge. This comprehensive guide has equipped you with multiple approaches and examples to strengthen your understanding and help you ace any fraction division problem that comes your way. Remember to practice regularly and don't hesitate to review these methods until you're comfortable with the process. With consistent effort, fraction division will become second nature!
Latest Posts
Latest Posts
-
3 Hour 50 Minute Marathon Pace
May 12, 2025
-
Can You Tan With A Uv Of 6
May 12, 2025
-
720 Square Inches To Square Feet
May 12, 2025
-
How Much 57 Stone Do I Need
May 12, 2025
-
How Long To Read 20 Pages
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Divided By 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.