1 3 Divided By 1 3 In Fraction
Treneri
May 11, 2025 · 5 min read
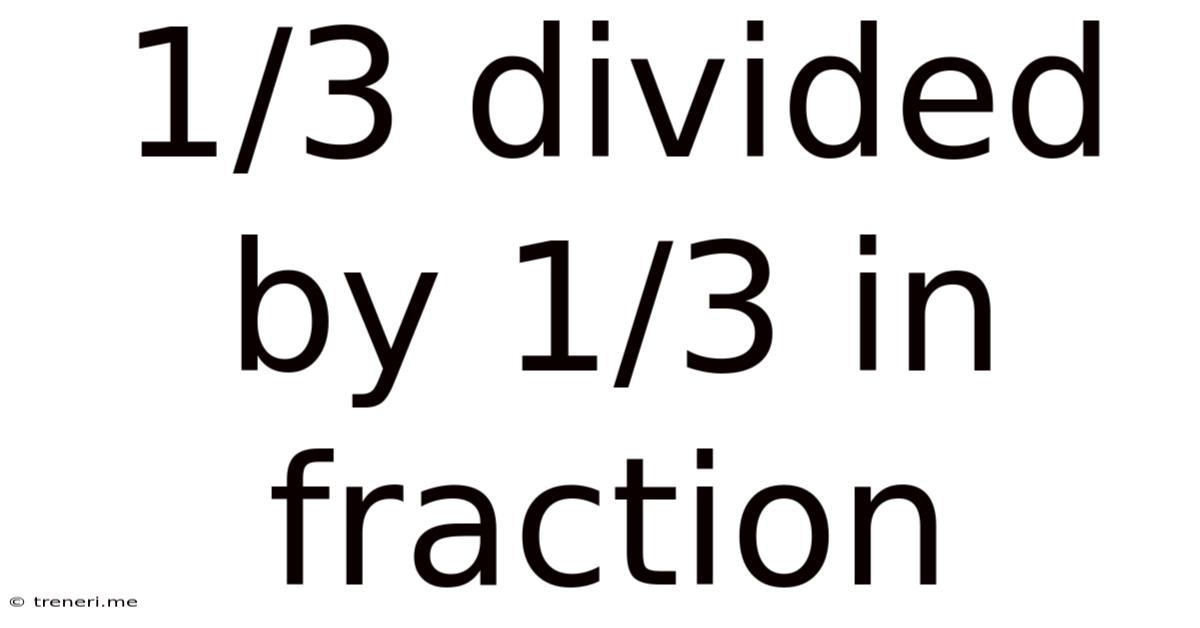
Table of Contents
1⅓ Divided by 1⅓ in Fraction: A Comprehensive Guide
Understanding fraction division can be tricky, but mastering it opens doors to solving a wide range of mathematical problems. This comprehensive guide will walk you through the process of dividing 1⅓ by 1⅓, explaining the concepts in detail and providing you with practical examples. We'll explore different methods, ensuring you grasp the fundamental principles and can confidently tackle similar fraction division problems in the future.
Understanding Fractions
Before diving into the division problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, representing the number of parts you have.
- Denominator: The bottom number, representing the total number of parts the whole is divided into.
For example, in the fraction ¾, the numerator is 3 (you have 3 parts), and the denominator is 4 (the whole is divided into 4 equal parts).
Converting Mixed Numbers to Improper Fractions
Our problem involves a mixed number, 1⅓. A mixed number combines a whole number and a fraction. To perform division more easily, we need to convert this mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
Here's how to convert 1⅓ to an improper fraction:
- Multiply the whole number by the denominator: 1 * 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: 3
Therefore, 1⅓ is equal to the improper fraction ⁴⁄₃.
Dividing Fractions: The Reciprocal Method
The most common method for dividing fractions involves using reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of ¾ is ⁴⁄₃.
To divide fractions, we follow these steps:
- Convert any mixed numbers to improper fractions: As we did above, converting 1⅓ to ⁴⁄₃.
- Change the division sign to a multiplication sign: This is the key step in the reciprocal method.
- Replace the second fraction with its reciprocal: Flip the second fraction.
- Multiply the numerators together: Multiply the top numbers.
- Multiply the denominators together: Multiply the bottom numbers.
- Simplify the resulting fraction (if possible): Reduce the fraction to its lowest terms.
Let's apply this to our problem: 1⅓ ÷ 1⅓
- Convert to improper fractions: ⁴⁄₃ ÷ ⁴⁄₃
- Change to multiplication: ⁴⁄₃ ×
- Use the reciprocal: ⁴⁄₃ × ³⁄₄
- Multiply numerators: 4 × 3 = 12
- Multiply denominators: 3 × 4 = 12
- Simplify: ¹²⁄₁₂ simplifies to 1
Therefore, 1⅓ ÷ 1⅓ = 1
Alternative Method: Using Decimal Representation
While the reciprocal method is generally preferred for fraction division, we can also solve this problem using decimal representation. First, convert the mixed number 1⅓ into its decimal equivalent.
1⅓ = 1 + (1/3) ≈ 1 + 0.3333... ≈ 1.3333...
Now, divide 1.3333... by 1.3333...
1.3333... ÷ 1.3333... = 1
This method provides a good approximation, especially when dealing with repeating decimals. However, the reciprocal method is more precise when dealing with exact fractions.
Why Understanding Fraction Division is Important
Mastering fraction division is crucial for several reasons:
- Foundation for Advanced Math: It's a building block for more complex mathematical concepts encountered in algebra, calculus, and other higher-level math courses.
- Real-World Applications: Many real-world scenarios involve dividing fractions, such as dividing ingredients in recipes, calculating distances, or working with measurements in construction and engineering.
- Problem-Solving Skills: Practicing fraction division improves your overall problem-solving abilities and analytical thinking.
- Improved Mathematical Fluency: Regular practice enhances your mathematical intuition and confidence.
Practicing Fraction Division: Similar Problems
To solidify your understanding, let's explore a few more examples of fraction division problems:
Example 1: 2²/₃ ÷ 1²/₃
- Convert to improper fractions: ⁸⁄₃ ÷ ⁵⁄₃
- Change to multiplication: ⁸⁄₃ ×
- Use the reciprocal: ⁸⁄₃ × ³⁄₅
- Multiply numerators: 8 × 3 = 24
- Multiply denominators: 3 × 5 = 15
- Simplify: ²⁴⁄₁₅ simplifies to ⁸⁄₅ or 1⅗
Therefore, 2²/₃ ÷ 1²/₃ = ⁸⁄₅ or 1⅗
Example 2: 3½ ÷ 2
- Convert to improper fractions: ⁷⁄₂ ÷ ²⁄₁
- Change to multiplication: ⁷⁄₂ ×
- Use the reciprocal: ⁷⁄₂ × ¹⁄₂
- Multiply numerators: 7 × 1 = 7
- Multiply denominators: 2 × 2 = 4
- Simplify: ⁷⁄₄ or 1¾
Therefore, 3½ ÷ 2 = ⁷⁄₄ or 1¾
Troubleshooting Common Mistakes in Fraction Division
Many students encounter common mistakes when working with fractions. Let's address some of them:
- Forgetting to use the reciprocal: Remember, dividing by a fraction is the same as multiplying by its reciprocal. Failing to flip the second fraction is a frequent error.
- Incorrectly converting mixed numbers: Always convert mixed numbers to improper fractions before performing division. An improper fraction simplifies the calculation process.
- Errors in simplifying fractions: Always reduce your final answer to its simplest form. Improper fractions can sometimes be converted back to mixed numbers for easier interpretation.
- Multiplication errors: Double-check your multiplication of numerators and denominators to avoid careless mistakes.
By paying close attention to these points and practicing regularly, you can significantly improve your accuracy in fraction division.
Conclusion: Mastering Fraction Division
Dividing fractions, even those involving mixed numbers like 1⅓ ÷ 1⅓, is achievable with a systematic approach. The reciprocal method, explained in detail above, provides a clear, efficient way to tackle these problems. By understanding the underlying principles and practicing consistently, you'll build your confidence and master this essential mathematical skill, opening doors to success in more advanced mathematical pursuits. Remember to always check your work and simplify your answer to its lowest terms. With practice, fraction division will become second nature.
Latest Posts
Latest Posts
-
How Long Is 72 Business Hours
May 12, 2025
-
El 5 Por Ciento De 25
May 12, 2025
-
How Many Hours Is In Two Weeks
May 12, 2025
-
How Many Days Since January 1 2022
May 12, 2025
-
How To Calculate The Concentration Of Protein From Absorbance
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 1 3 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.