1 4 X 1 3 As A Fraction
Treneri
May 13, 2025 · 4 min read
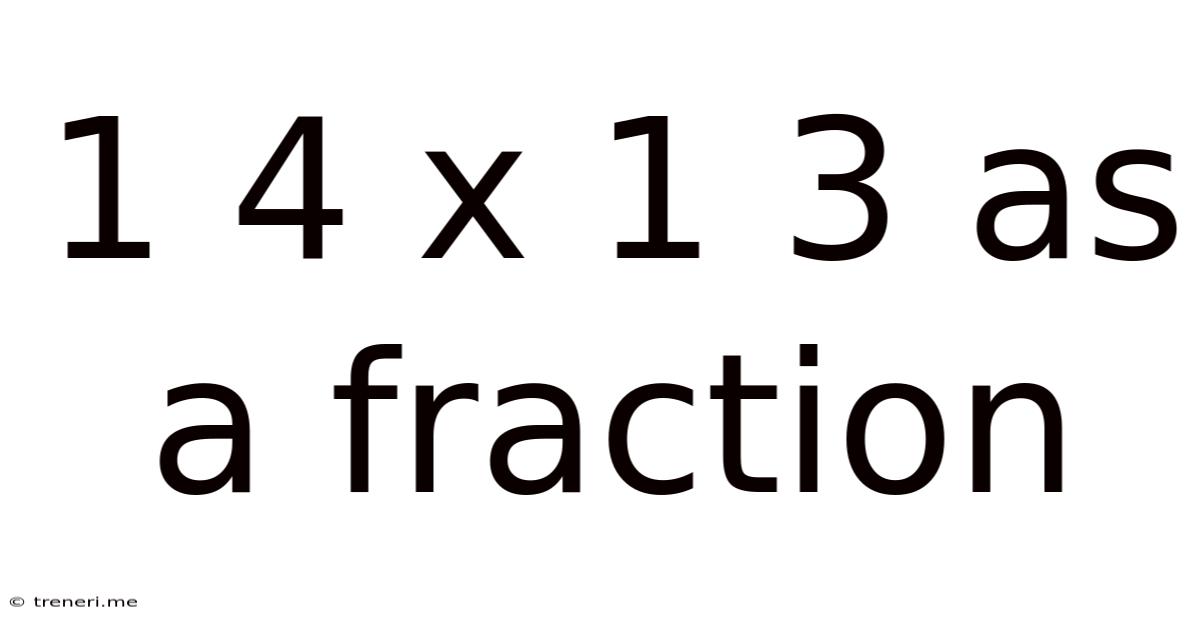
Table of Contents
1 ¼ x 1⅓ as a Fraction: A Comprehensive Guide
Understanding fraction multiplication can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of solving 1 ¼ x 1⅓ as a fraction, explaining each step in detail and providing valuable insights into working with fractions in general. We'll explore different methods, address common pitfalls, and offer practical applications to solidify your understanding.
Converting Mixed Numbers to Improper Fractions
Before we tackle the multiplication, we need to convert our mixed numbers (numbers with both a whole number and a fraction) into improper fractions (fractions where the numerator is greater than the denominator). This makes the multiplication process much simpler.
Step 1: Converting 1 ¼
- Multiply the whole number by the denominator: 1 x 4 = 4
- Add the numerator: 4 + 1 = 5
- Keep the same denominator: The denominator remains 4.
Therefore, 1 ¼ is equivalent to 5/4.
Step 2: Converting 1⅓
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator: 3 + 1 = 4
- Keep the same denominator: The denominator remains 3.
Therefore, 1⅓ is equivalent to 4/3.
Multiplying the Improper Fractions
Now that we've converted our mixed numbers, we can proceed with the multiplication. Remember the simple rule: multiply the numerators together and multiply the denominators together.
Step 3: Multiplying Numerators and Denominators
- Multiply the numerators: 5 x 4 = 20
- Multiply the denominators: 4 x 3 = 12
This gives us the improper fraction 20/12.
Simplifying the Fraction
Our answer, 20/12, is an improper fraction, and it can be simplified. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Step 4: Finding the Greatest Common Divisor (GCD)
The GCD of 20 and 12 is 4. This means we can divide both the numerator and the denominator by 4 without changing the value of the fraction.
Step 5: Simplifying to the Lowest Terms
- Divide the numerator by the GCD: 20 ÷ 4 = 5
- Divide the denominator by the GCD: 12 ÷ 4 = 3
This simplifies our fraction to 5/3.
Converting Back to a Mixed Number (Optional)
While 5/3 is a perfectly acceptable answer, we can also convert it back to a mixed number if desired.
Step 6: Converting the Improper Fraction to a Mixed Number
- Divide the numerator by the denominator: 5 ÷ 3 = 1 with a remainder of 2
- The whole number is the quotient: 1
- The numerator of the fraction is the remainder: 2
- The denominator remains the same: 3
Therefore, 5/3 is equivalent to 1²/₃.
Alternative Methods: Using Decimal Multiplication
While the fraction method is generally preferred for accuracy and understanding fundamental mathematical principles, you can also solve this problem using decimal multiplication.
Step 1: Converting Fractions to Decimals
Convert 1 ¼ to its decimal equivalent: 1.25 Convert 1⅓ to its decimal equivalent: 1.333... (This is a repeating decimal)
Step 2: Multiplying the Decimals
Multiply 1.25 by 1.333... This will give you an approximate answer due to the repeating decimal. The result will be approximately 1.666...
Step 3: Converting the Decimal Back to a Fraction (Approximate)
Converting the approximate decimal 1.666... back to a fraction will yield an approximation of 5/3. This method is less accurate than using the fraction method directly, particularly when dealing with repeating decimals.
Practical Applications and Real-World Examples
Understanding fraction multiplication is essential in various real-world situations:
- Baking and Cooking: Recipes often require fractional measurements of ingredients. Accurately multiplying fractions is crucial for scaling recipes up or down.
- Construction and Engineering: Precise measurements and calculations are vital in construction and engineering projects. Fractions play a critical role in ensuring accuracy.
- Finance and Accounting: Calculating interest rates, discounts, and proportions often involve working with fractions.
- Sewing and Tailoring: Pattern making and fabric cutting necessitate accurate fractional measurements.
Common Mistakes to Avoid
- Forgetting to convert mixed numbers to improper fractions before multiplying: This is a common error that leads to incorrect results. Always convert mixed numbers to improper fractions first.
- Not simplifying the resulting fraction: Always simplify the fraction to its lowest terms for a concise and accurate answer.
- Making mistakes in multiplication: Double-check your multiplication to avoid errors.
- Incorrectly converting between fractions and decimals: Be cautious when converting between fractions and decimals, especially with repeating decimals.
Conclusion: Mastering Fraction Multiplication
Solving 1 ¼ x 1⅓ as a fraction involves a straightforward process: convert mixed numbers to improper fractions, multiply the numerators and denominators, and simplify the resulting fraction. This comprehensive guide provides a clear, step-by-step approach to ensure accurate calculations and a deeper understanding of fraction multiplication. Remember to practice regularly and avoid common mistakes to solidify your skills and confidently tackle more complex fraction problems in various real-world scenarios. The ability to work fluently with fractions is a cornerstone of mathematical proficiency, with far-reaching applications across many disciplines. By mastering this fundamental skill, you'll enhance your problem-solving abilities and open doors to a wider range of mathematical challenges.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 48 And 56
May 13, 2025
-
Cuanto Es 53 Kg En Libras
May 13, 2025
-
90 Days After September 6 2024
May 13, 2025
-
What Is 10 Percent Of 38000
May 13, 2025
-
1 3 To The 3rd Power
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1 4 X 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.