1/5 + 3/4 As A Fraction
Treneri
May 11, 2025 · 5 min read
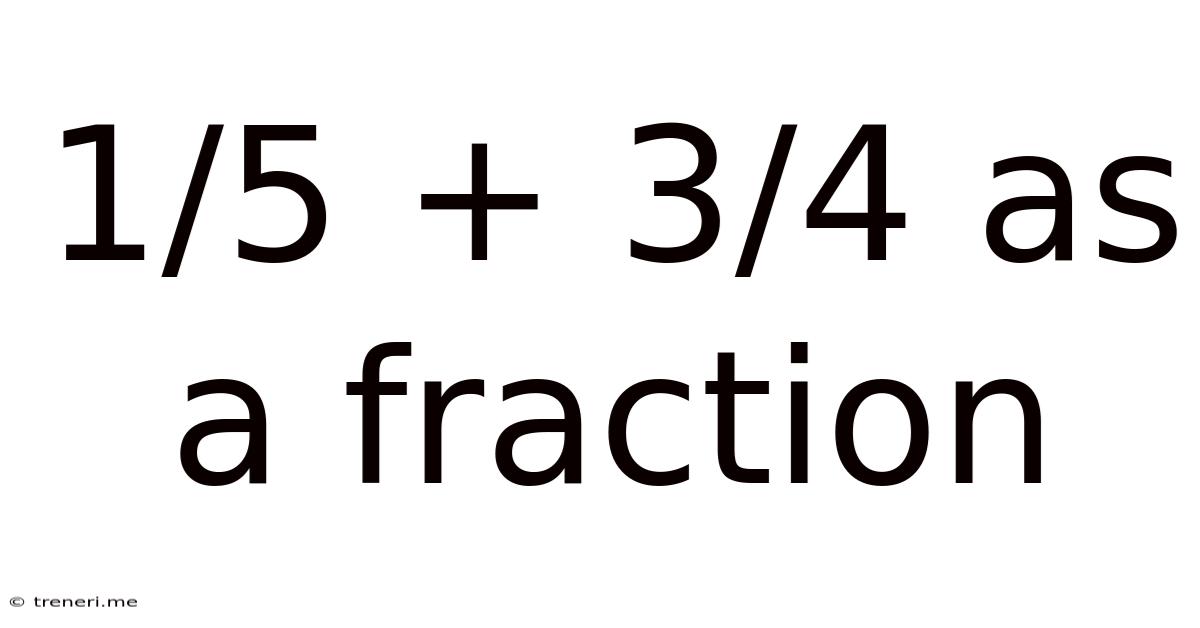
Table of Contents
1/5 + 3/4 as a Fraction: A Comprehensive Guide to Adding Fractions
Adding fractions might seem like a simple arithmetic task, but mastering it forms the foundation for more complex mathematical concepts. This comprehensive guide will delve into the process of adding 1/5 and 3/4, explaining the steps involved, providing alternative methods, and exploring the broader context of fraction addition. We'll also touch upon practical applications and address common misconceptions.
Understanding Fractions
Before we tackle the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the context of our problem, 1/5 signifies one part out of five equal parts, and 3/4 signifies three parts out of four equal parts. These fractions have different denominators, meaning they represent parts of wholes that are divided into different numbers of pieces. This difference necessitates a crucial step before we can add them.
Finding a Common Denominator
The core principle of adding fractions is that we can only directly add the numerators when the denominators are the same. Since 1/5 and 3/4 have different denominators (5 and 4), we must find a common denominator. This is a number that is a multiple of both 5 and 4.
Several methods exist to find the least common denominator (LCD), the smallest number that both denominators divide into evenly. Here are two common approaches:
1. Listing Multiples
List the multiples of each denominator until you find a common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
Notice that 20 appears in both lists. Therefore, 20 is the least common denominator (LCD) for 1/5 and 3/4.
2. Prime Factorization
This method is particularly useful for larger denominators. It involves breaking down each denominator into its prime factors.
- 5 = 5 (5 is a prime number)
- 4 = 2 x 2 = 2²
To find the LCD, take the highest power of each prime factor present in either factorization and multiply them together. In this case:
LCD = 2² x 5 = 4 x 5 = 20
Converting Fractions to Equivalent Fractions
Now that we have the LCD (20), we need to convert both 1/5 and 3/4 into equivalent fractions with a denominator of 20. This is done by multiplying both the numerator and the denominator of each fraction by the appropriate factor.
- For 1/5: To get a denominator of 20, we multiply both the numerator and denominator by 4 (since 5 x 4 = 20):
(1 x 4) / (5 x 4) = 4/20
- For 3/4: To get a denominator of 20, we multiply both the numerator and denominator by 5 (since 4 x 5 = 20):
(3 x 5) / (4 x 5) = 15/20
Adding the Fractions
With both fractions now having the same denominator (20), we can add them by simply adding the numerators and keeping the denominator the same:
4/20 + 15/20 = (4 + 15) / 20 = 19/20
Therefore, the sum of 1/5 and 3/4 is 19/20.
Simplifying Fractions (If Necessary)
In this case, 19/20 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In other words, no number other than 1 divides both the numerator and denominator evenly. If the resulting fraction after addition wasn't in its simplest form, we'd need to find the GCD and divide both the numerator and denominator by it.
Visual Representation
Understanding fractions can be enhanced through visual aids. Imagine a pizza cut into 20 slices. 1/5 of the pizza would be 4 slices (20/5 = 4), and 3/4 of the pizza would be 15 slices (20/4 = 15). Adding these together (4 + 15 = 19) gives us 19 out of 20 slices, confirming our result of 19/20.
Alternative Methods: Using a Calculator
While understanding the underlying principles is crucial, you can also use a calculator to verify your results or solve more complex fraction problems. Many calculators have a dedicated fraction function. Simply input the fractions, use the addition operator, and the calculator will provide the answer, often in its simplest form.
Practical Applications of Fraction Addition
Adding fractions isn't just a theoretical exercise; it has numerous practical applications in daily life and various fields:
- Cooking and Baking: Recipes often require fractions of ingredients. Adding fractions helps you accurately measure ingredients.
- Construction and Engineering: Precise measurements are essential in construction and engineering, often involving fractions of units like inches or meters.
- Finance and Budgeting: Understanding fractions is vital for calculating percentages, interest rates, and managing budgets.
- Science and Data Analysis: Fractions are used extensively in scientific measurements and calculations, especially in areas like chemistry and physics.
Common Mistakes to Avoid
Several common errors can arise when adding fractions:
- Forgetting to find a common denominator: This is the most frequent mistake. Always ensure both fractions have the same denominator before adding the numerators.
- Incorrectly finding the common denominator: Carefully choose the LCD using either method outlined above to avoid errors.
- Adding denominators: Remember, you only add the numerators; the denominator remains the same after the addition.
- Not simplifying the final answer: Always check if the resulting fraction can be simplified.
Conclusion: Mastering Fraction Addition
Adding fractions, even seemingly simple ones like 1/5 + 3/4, requires a systematic approach. By understanding the concepts of common denominators, equivalent fractions, and simplification, you can confidently tackle fraction addition problems. Remember to practice regularly to build your skills and avoid common pitfalls. This foundational knowledge empowers you to solve more complex mathematical problems and apply this essential skill in various aspects of life. From baking a cake to understanding financial data, mastering fraction addition opens up a wider world of possibilities. Remember to always double-check your work and utilize visual aids when needed to reinforce your understanding. The more you practice, the more confident and proficient you will become.
Latest Posts
Latest Posts
-
5 Divided By 4 5 As A Fraction
May 13, 2025
-
Formula De Grados Fahrenheit A Centigrados
May 13, 2025
-
What Does Uv Have To Be To Tan
May 13, 2025
-
What Is The Multiplicative Inverse Of 1 2
May 13, 2025
-
30 Days From December 8 2023
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1/5 + 3/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.