1/8 Divided By 3/4 In Fraction Form
Treneri
May 13, 2025 · 5 min read
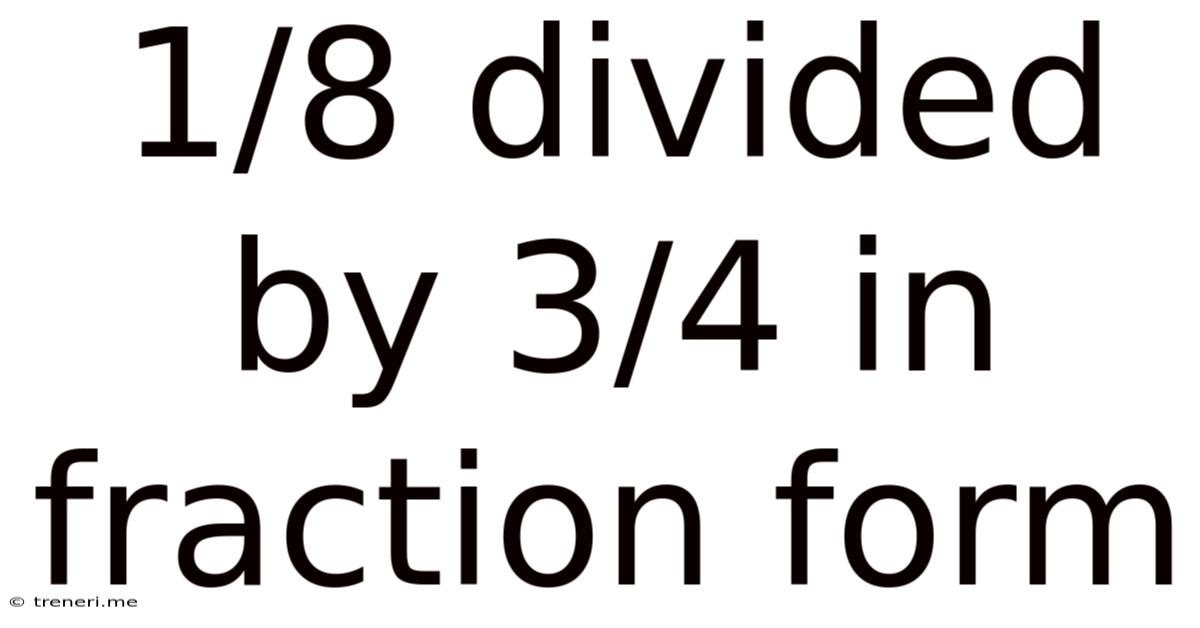
Table of Contents
1/8 Divided by 3/4 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 1/8 by 3/4, explaining the concepts involved and providing various approaches to solve this problem and similar fraction division problems. We'll also delve into the underlying mathematical principles and explore practical applications.
Understanding Fraction Division
Before tackling the specific problem of 1/8 ÷ 3/4, let's establish a solid foundation in fraction division. The key concept is to understand that dividing by a fraction is the same as multiplying by its reciprocal.
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3. This fundamental rule transforms a division problem into a multiplication problem, which is generally easier to handle.
Therefore, the general rule for dividing fractions is:
a/b ÷ c/d = a/b * d/c
Where 'a', 'b', 'c', and 'd' represent numbers, and 'b' and 'c' are not zero (as division by zero is undefined).
Solving 1/8 Divided by 3/4
Now, let's apply this rule to our specific problem: 1/8 ÷ 3/4.
Step 1: Find the reciprocal of the second fraction.
The reciprocal of 3/4 is 4/3.
Step 2: Change the division problem to a multiplication problem.
1/8 ÷ 3/4 becomes 1/8 * 4/3.
Step 3: Multiply the numerators (top numbers) together.
1 * 4 = 4
Step 4: Multiply the denominators (bottom numbers) together.
8 * 3 = 24
Step 5: Simplify the resulting fraction.
The fraction we get is 4/24. This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 4 and 24 is 4. Dividing both the numerator and the denominator by 4 gives us:
4/24 = 1/6
Therefore, 1/8 ÷ 3/4 = 1/6
Alternative Methods and Visual Representations
While the reciprocal method is the most efficient, there are alternative approaches that can help solidify your understanding.
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions before dividing. While slightly more complex than the reciprocal method, it provides a different perspective on fraction division.
- Find a common denominator: The least common multiple (LCM) of 8 and 4 is 8.
- Convert the fractions to equivalent fractions with the common denominator: 1/8 remains 1/8, and 3/4 becomes 6/8.
- Divide the numerators: 1 ÷ 6 = 1/6
This method arrives at the same answer: 1/6. However, the reciprocal method is generally preferred for its simplicity and efficiency.
Visual Representation
Visualizing the problem can be beneficial, especially for beginners. Imagine a pizza cut into 8 slices. 1/8 represents one slice. Dividing this slice into 3/4 portions means conceptually dividing that single slice into three quarters. The result is a much smaller fraction, representing 1/6 of the original pizza.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving mathematical problems; it has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often require fractions of ingredients. If a recipe calls for 3/4 cup of flour and you only want to make 1/8 of the recipe, you'll need to divide 3/4 by 8 to find the required amount of flour.
- Sewing and Crafting: Cutting fabric or other materials often involves precise measurements using fractions. Dividing fractional lengths is crucial for accurate cutting.
- Construction and Engineering: Many construction and engineering projects involve calculations with fractions and precise measurements. Dividing fractions is essential for accurate calculations in these fields.
- Data Analysis: In data analysis and statistics, you might encounter situations where you need to divide fractional values. For example, if you're analyzing data representing parts of a whole, you might need to divide fractions to understand proportions or relationships.
Expanding on Fraction Division: More Complex Scenarios
While the problem 1/8 ÷ 3/4 is relatively straightforward, let's consider more complex scenarios to further enhance your understanding of fraction division.
-
Dividing Mixed Numbers: Mixed numbers are numbers with a whole number part and a fractional part (e.g., 2 1/2). To divide mixed numbers, first convert them into improper fractions (fractions where the numerator is larger than the denominator). Then apply the reciprocal method as described above.
-
Dividing Fractions with Different Signs: If either the dividend or the divisor is negative, apply the rules of signed number division. Remember that a positive number divided by a negative number results in a negative number, and a negative number divided by a negative number results in a positive number.
-
Dividing Fractions with Variables: Algebra introduces the concept of dividing fractions containing variables. The principles remain the same; find the reciprocal of the second fraction and then multiply.
Troubleshooting Common Mistakes
Common mistakes when dividing fractions include:
- Forgetting to find the reciprocal: Remember that you must find the reciprocal of the second fraction before multiplying.
- Incorrect simplification: Always simplify your final answer to its lowest terms by finding the greatest common divisor of the numerator and the denominator.
- Mixing up multiplication and division rules: Multiplication and division of fractions have distinct rules. Pay close attention to which operation you're performing.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial skill in mathematics and has widespread practical applications. By understanding the reciprocal method, practicing different scenarios, and avoiding common mistakes, you can confidently tackle fraction division problems of any complexity. Remember that consistent practice and a solid grasp of the underlying principles are key to achieving proficiency. This guide provides a thorough foundation, and with further practice, you can solidify your understanding and become adept at solving fraction division problems. Remember to always check your work and simplify your answers to their lowest terms for accurate and efficient results.
Latest Posts
Latest Posts
-
Whats The Square Root Of 19
May 13, 2025
-
Monthly Vs Bi Weekly Vs Weekly Mortgage Calculator
May 13, 2025
-
How To Find A Missing Side Of A Rectangle
May 13, 2025
-
Greatest Common Factor Of 4 And 9
May 13, 2025
-
Z Score For 92 Confidence Interval
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1/8 Divided By 3/4 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.