1 As A Power Of 10
Treneri
May 14, 2025 · 5 min read
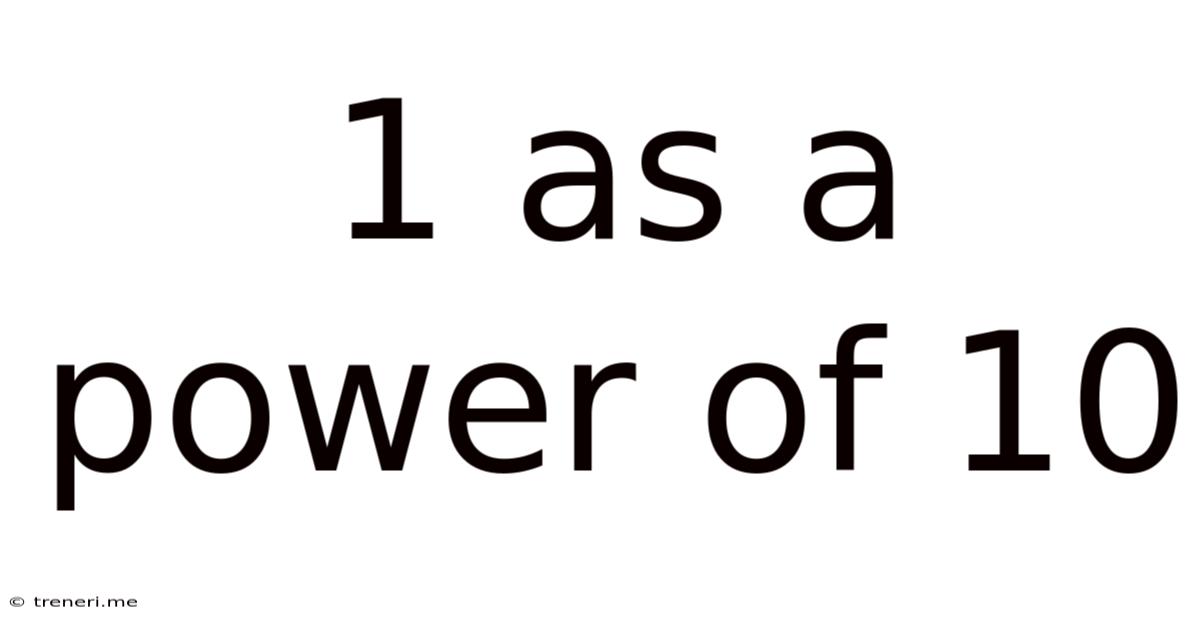
Table of Contents
1 as a Power of 10: Exploring the Mathematical Identity and its Implications
The seemingly simple statement "1 is a power of 10" might initially appear trivial. However, a deeper exploration reveals fascinating connections within mathematics, computer science, and even our understanding of numerical representation. This article delves into the mathematical identity of 1 as 10<sup>0</sup>, unpacking its implications and exploring its relevance across various fields.
Understanding Exponential Notation
Before diving into the specifics of 1 as a power of 10, let's establish a firm understanding of exponential notation. Exponential notation, also known as scientific notation, provides a concise way to represent very large or very small numbers. It's built upon the concept of a base raised to an exponent. For example, in the expression 10<sup>3</sup>, 10 is the base and 3 is the exponent. This signifies 10 multiplied by itself three times (10 × 10 × 10 = 1000).
The Significance of the Exponent
The exponent dictates how many times the base is multiplied by itself. A positive exponent indicates repeated multiplication, while a negative exponent signifies repeated division. For instance:
- 10<sup>2</sup> = 100
- 10<sup>1</sup> = 10
- 10<sup>0</sup> = 1
- 10<sup>-1</sup> = 0.1
- 10<sup>-2</sup> = 0.01
The crucial point here is the role of the exponent 0. Any non-zero number raised to the power of 0 always equals 1. This is a fundamental rule in mathematics.
1 as 10<sup>0</sup>: The Mathematical Identity
The statement "1 is a power of 10" is directly derived from the mathematical identity 10<sup>0</sup> = 1. This identity is not arbitrary; it's a consistent consequence of the rules governing exponents. Consider the pattern of decreasing exponents:
10<sup>3</sup> = 1000 10<sup>2</sup> = 100 10<sup>1</sup> = 10
Notice that each time the exponent decreases by 1, the result is divided by 10. Following this pattern logically, to reach 10<sup>0</sup>, we must divide 10<sup>1</sup> (which is 10) by 10. This yields 1. This consistent pattern reinforces the validity of 10<sup>0</sup> = 1.
The Zero Exponent Rule: A Deeper Dive
The zero exponent rule isn't simply a convenient convention; it's mathematically sound and consistent with the properties of exponents. It's crucial for maintaining the consistency of exponential operations. Consider the following:
x<sup>m</sup> / x<sup>n</sup> = x<sup>(m-n)</sup>
If we let m = n, we get:
x<sup>m</sup> / x<sup>m</sup> = x<sup>(m-m)</sup> = x<sup>0</sup>
Since any number divided by itself equals 1 (excluding division by zero), we conclude that x<sup>0</sup> = 1, provided x ≠ 0. This demonstrates the mathematical rigor underpinning the zero exponent rule.
Implications Across Different Fields
The seemingly simple identity 10<sup>0</sup> = 1 has significant implications in various fields:
1. Computer Science and Binary Representation
In computer science, numbers are represented in binary (base-2) rather than decimal (base-10). However, the concept of the zero exponent remains crucial. The binary representation of 1 is 10<sup>0</sup> in binary, which is equivalent to 2<sup>0</sup> = 1 in decimal. This fundamental concept underpins how computers handle numerical calculations and data storage.
The ability to represent 1 as a power of any base (including binary) is fundamental to how computers perform arithmetic operations, memory addressing, and data manipulation. It’s a cornerstone of digital logic and Boolean algebra.
2. Scientific Notation and Large Numbers
Scientific notation utilizes powers of 10 to represent extremely large or small numbers concisely. The number 1 acts as a crucial baseline. For example:
- The speed of light is approximately 3 × 10<sup>8</sup> meters per second.
- The mass of an electron is approximately 9.1 × 10<sup>-31</sup> kilograms.
Without the ability to represent 1 as 10<sup>0</sup>, the entire system of scientific notation would be inconsistent and much harder to manage.
3. Logarithms and Exponential Functions
Logarithms are the inverse functions of exponential functions. The logarithm base 10 of 1 (log<sub>10</sub>1) is 0. This directly relates to the fact that 10<sup>0</sup> = 1. The understanding of 1 as 10<sup>0</sup> is essential for comprehending logarithmic scales frequently used in various fields such as acoustics, chemistry, and seismology. These scales help represent large ranges of values in a manageable way.
4. Mathematics and Number Theory
The identity 10<sup>0</sup> = 1 plays a critical role in various mathematical theorems and proofs. It serves as a foundational element in number theory, algebra, and calculus. Many mathematical relationships and identities rely on the consistency of this fundamental rule. For instance, in the study of series and sequences, the term with the zeroth power often serves as a starting point or baseline.
5. Data Analysis and Statistics
In data analysis and statistics, the number 1 often represents a baseline or reference point. For example, in probability, an event with a probability of 1 is a certain event. This connects to the idea of 1 as a power of 10, highlighting its significance in defining and understanding fundamental concepts in these fields.
The Uniqueness of 1: A Mathematical Cornerstone
The number 1 holds a unique position in mathematics. It's the multiplicative identity, meaning any number multiplied by 1 remains unchanged. This property, combined with its representation as 10<sup>0</sup>, solidifies its fundamental role in numerical systems and mathematical operations. Its importance isn't simply limited to base-10 systems; it’s universally applicable across all numerical bases.
Conclusion: Beyond the Obvious
While the statement "1 is a power of 10" may seem trivial at first glance, a thorough examination reveals its deep-seated significance across numerous branches of mathematics and related fields. Its role as a foundation for exponential notation, its impact on computer science, and its use in scientific notation and logarithmic scales demonstrate its fundamental importance in our understanding of numbers and their manipulation. The seemingly simple identity 10<sup>0</sup> = 1 acts as a powerful, yet often overlooked, building block in our quantitative world. Understanding this identity provides a deeper appreciation for the underlying principles that govern our mathematical frameworks and their applications.
Latest Posts
Latest Posts
-
Can You Get Tan When The Uv Is 6
May 14, 2025
-
How Much More Time Until 3 30
May 14, 2025
-
320 Grams Of Pasta To Cups
May 14, 2025
-
How Much Gas Is 20 Miles
May 14, 2025
-
What Is 1 3 Of 70
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1 As A Power Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.