1 Divided By 1 3 As A Fraction
Treneri
May 13, 2025 · 5 min read
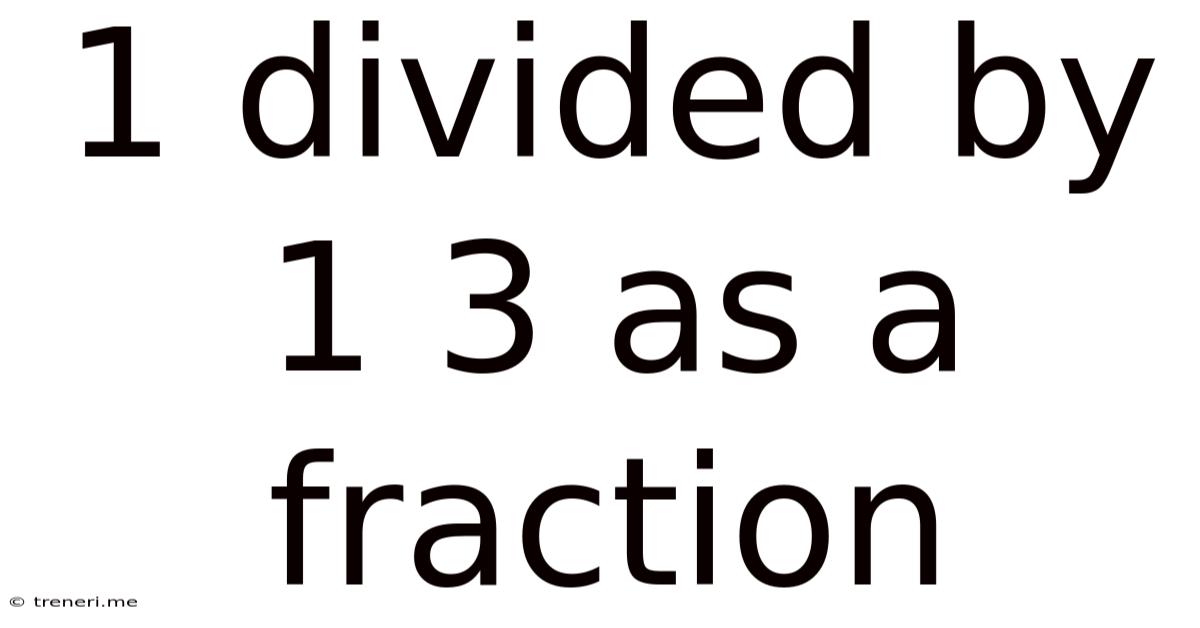
Table of Contents
1 Divided by 1 ⅓ as a Fraction: A Comprehensive Guide
Understanding how to divide by fractions is a fundamental skill in mathematics. This seemingly simple calculation, 1 divided by 1 ⅓, can be approached in several ways, each offering valuable insights into fractional arithmetic. This guide will explore these methods, providing a clear and comprehensive explanation suitable for all levels of mathematical understanding. We'll delve into the concepts behind the process, emphasizing practical applications and highlighting common pitfalls to avoid. By the end, you'll not only know the answer but also possess a deeper understanding of fraction division.
Understanding the Problem: 1 ÷ 1 ⅓
Before diving into the solutions, let's clarify the problem: We need to calculate 1 divided by 1 ⅓. This can be represented mathematically as:
1 ÷ 1 ⅓
This expression involves dividing a whole number (1) by a mixed number (1 ⅓). Mixed numbers, like 1 ⅓, combine a whole number and a fraction. To perform the division effectively, we need to convert this mixed number into an improper fraction.
Converting Mixed Numbers to Improper Fractions
A mixed number represents a whole number plus a fraction. To convert a mixed number to an improper fraction, we follow these steps:
-
Multiply the whole number by the denominator of the fraction: In our case, 1 (whole number) multiplied by 3 (denominator) equals 3.
-
Add the numerator of the fraction to the result: Add 1 (numerator) to 3, giving us 4.
-
Keep the same denominator: The denominator remains 3.
Therefore, 1 ⅓ converts to the improper fraction ⁴⁄₃.
Our problem now becomes:
1 ÷ ⁴⁄₃
Method 1: Reciprocals and Multiplication
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of ⁴⁄₃ is ³⁄₄.
So, our problem transforms into:
1 × ³⁄₄
Multiplying a whole number by a fraction is straightforward:
1 × ³⁄₄ = ³⁄₄
Therefore, 1 divided by 1 ⅓ equals ³⁄₄.
Method 2: Converting to a Common Denominator
This method involves converting the whole number into a fraction with the same denominator as the mixed number. This approach offers a different perspective on fraction division.
-
Convert the whole number to a fraction: We can express 1 as ³⁄₃ (any number divided by itself equals 1).
-
Rewrite the problem: Our problem now looks like this: ³⁄₃ ÷ ⁴⁄₃
-
Divide the numerators and the denominators: When dividing fractions with the same denominator, we simply divide the numerators. This gives us:
³⁄₄
Therefore, using this method, we again arrive at the answer ³⁄₄.
Method 3: Long Division with Fractions
While less efficient for this particular problem, the long division method provides a deeper understanding of the underlying process. This method is particularly helpful when dealing with more complex fraction divisions.
-
Convert the mixed number to an improper fraction: As before, 1 ⅓ becomes ⁴⁄₃.
-
Set up the long division: The problem becomes: 1 ÷ ⁴⁄₃, which can be rewritten as:
1 ÷ ⁴⁄₃ -
Invert the divisor and multiply: This step involves multiplying 1 by the reciprocal of ⁴⁄₃, which is ³⁄₄, giving us:
1 × ³⁄₄ = ³⁄₄
This method reiterates the result: ³⁄₄
Understanding the Result: ³⁄₄
The solution, ³⁄₄, signifies that one whole is divided into three equal parts, and we are taking four of those parts. It highlights the essence of fraction division.
Let’s visualize this: Imagine a pizza cut into 3 slices. You have a whole pizza (1). If you divide this pizza into servings, each representing ⅓ of a pizza, you have three servings. To get ⁴⁄₃ of a pizza (1 ⅓), you would need all three slices (1 whole pizza) and an extra third of a slice from a second pizza. Hence, one whole pizza (1) can provide only ¾ servings of the ⅓ pizza size.
Applications of Fraction Division
Understanding fraction division is crucial in various real-world applications, including:
- Baking and Cooking: Scaling recipes up or down often requires dividing fractional quantities.
- Construction and Engineering: Precise measurements and calculations frequently involve fractions.
- Sewing and Quilting: Cutting fabric and creating patterns require accuracy in fractional measurements.
- Finance and Accounting: Dividing profits or expenses proportionally often requires working with fractions.
- Data analysis and statistics: Many calculations in these fields involve working with proportions and fractions.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect results when dividing fractions:
- Forgetting to convert mixed numbers: Failing to convert mixed numbers to improper fractions before dividing is a frequent error.
- Inverting the wrong fraction: Remember to invert the divisor (the fraction you are dividing by), not the dividend (the number being divided).
- Incorrect multiplication after inverting: Carefully multiply the numerators and denominators after inverting the divisor.
- Not simplifying the result: Always simplify the resulting fraction to its lowest terms.
Conclusion: Mastering Fraction Division
Dividing by fractions, while initially appearing complex, is a fundamental mathematical operation with numerous real-world applications. By understanding the different methods – using reciprocals, converting to common denominators, or employing long division – you can confidently tackle such problems. Remember to pay close attention to the steps involved, especially converting mixed numbers to improper fractions and carefully handling the multiplication after inverting the divisor. By mastering these techniques, you'll enhance your mathematical skills and successfully navigate various scenarios that require fraction division. Regular practice and attention to detail will solidify your understanding and improve your accuracy. Through consistent application, you'll gain confidence and efficiency in your approach to fraction division.
Latest Posts
Latest Posts
-
1 Cubic Yard Of Concrete Weight
May 13, 2025
-
Whats The Difference Between Milliliters And Milligrams
May 13, 2025
-
How Many Calories Do I Burn Biking 20 Miles
May 13, 2025
-
Calculate The Molality Of A Solution Formed By Adding
May 13, 2025
-
1968 To 2023 How Many Years
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.