1 Divided By 1 3 In Fraction
Treneri
May 14, 2025 · 4 min read
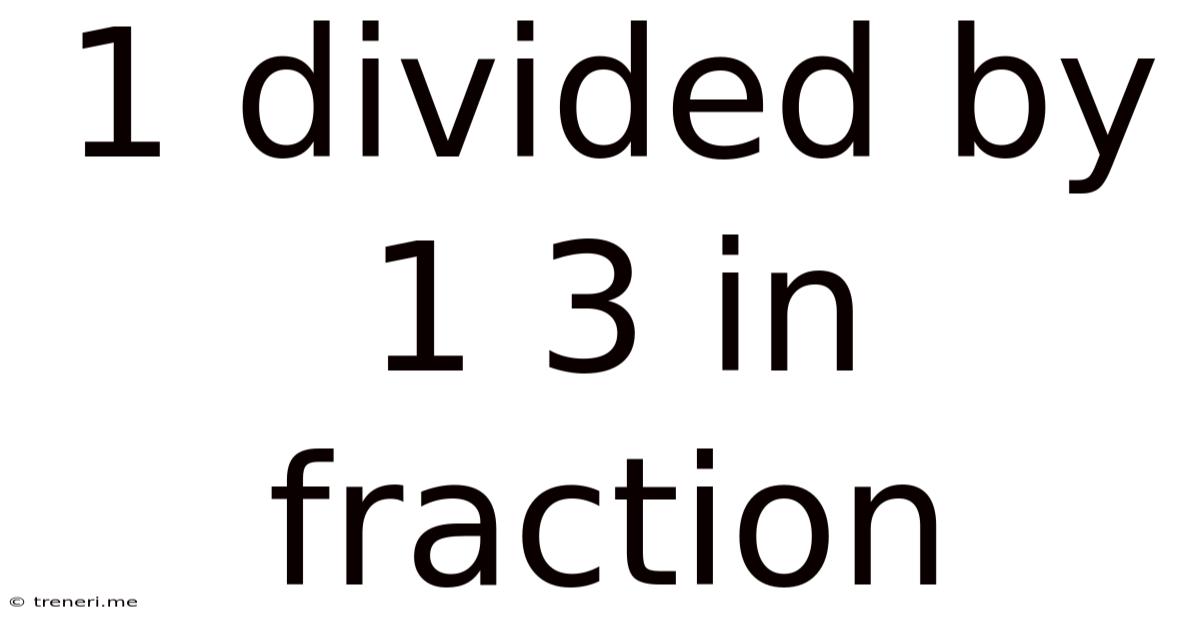
Table of Contents
1 Divided by 1 ⅓: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of solving 1 divided by 1 ⅓, explaining the underlying principles and offering various approaches to tackle similar problems. We'll delve into the intricacies of converting mixed numbers to improper fractions, the mechanics of reciprocal multiplication, and finally, simplifying the resulting fraction to its lowest terms. By the end, you’ll not only know the answer but also understand the why behind each step.
Understanding the Problem: 1 ÷ 1 ⅓
The problem, 1 ÷ 1 ⅓, presents us with a division problem involving a whole number (1) and a mixed number (1 ⅓). To solve this efficiently, we need to convert the mixed number into an improper fraction. This is a crucial step that will streamline the entire calculation.
What is a Mixed Number?
A mixed number combines a whole number and a fraction, representing a value greater than one. In our case, 1 ⅓ represents one whole unit and one-third of another unit.
Converting Mixed Numbers to Improper Fractions
Converting a mixed number to an improper fraction is the key to simplifying our division problem. The process involves:
- Multiplying: Multiply the whole number by the denominator of the fraction. (1 x 3 = 3)
- Adding: Add the result to the numerator of the fraction. (3 + 1 = 4)
- Keeping the Denominator: Retain the original denominator of the fraction.
Therefore, 1 ⅓ converts to the improper fraction ⁴⁄₃. Our problem now becomes: 1 ÷ ⁴⁄₃.
Dividing Fractions: The Reciprocal Method
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of ⁴⁄₃ is ³⁄₄.
This is a fundamental concept in fraction division. Instead of dividing by ⁴⁄₃, we will multiply by its reciprocal, ³⁄₄. This transforms our problem into:
1 x ³⁄₄
Solving the Problem: 1 x ³⁄₄
Multiplying a whole number by a fraction is straightforward:
- Convert the whole number to a fraction: Any whole number can be written as a fraction with a denominator of 1. So, 1 becomes ¹⁄₁.
- Multiply the numerators: Multiply the numerators of the two fractions (1 x 3 = 3).
- Multiply the denominators: Multiply the denominators of the two fractions (1 x 4 = 4).
This results in the fraction ³⁄₄.
Simplifying Fractions: Finding the Lowest Terms
While ³⁄₄ is a perfectly valid answer, it's good practice to always simplify fractions to their lowest terms. A fraction is in its lowest terms when the greatest common divisor (GCD) of the numerator and the denominator is 1.
In this case, the GCD of 3 and 4 is 1, meaning our fraction is already in its simplest form.
Alternative Methods: Using Decimal Conversions
While the reciprocal method is generally preferred for its efficiency and conceptual clarity, you can also solve this problem using decimal conversions.
- Convert the mixed number to a decimal: 1 ⅓ is equal to 1.333... (the 3s repeating infinitely).
- Perform the division: Divide 1 by 1.333... This will yield approximately 0.75.
- Convert the decimal back to a fraction: 0.75 is equivalent to ¾.
This method, however, can be less precise if you're dealing with repeating decimals and requires more steps. The reciprocal method offers a cleaner, more direct solution.
Practical Applications and Real-World Examples
Understanding fraction division is crucial in many real-world scenarios. Here are a few examples:
- Baking: Recipes often require fractional amounts of ingredients. Dividing ingredients equally among servings necessitates fraction division. For instance, if you have 1 cup of flour and need to divide it among 1 ⅓ servings, you’d need to calculate ¾ cup of flour per serving.
- Construction and Engineering: Precise measurements are paramount in these fields. Dividing lengths, areas, or volumes often involves fractions and requires accurate fraction division.
- Sewing and Tailoring: Pattern making and fabric cutting rely heavily on accurate measurements. Understanding fraction division ensures precise cutting and minimizes waste.
- Finance: Calculating interest rates, shares of ownership, or distributing profits often involves fractional calculations.
Expanding the Knowledge: More Complex Fraction Division Problems
The principles discussed here apply to more complex fraction division problems. Let's consider a slightly more challenging example: 2 ½ ÷ 1 ⅔
- Convert Mixed Numbers to Improper Fractions: 2 ½ becomes ⁵⁄₂ and 1 ⅔ becomes ⁵⁄₃
- Apply the Reciprocal Method: ⁵⁄₂ ÷ ⁵⁄₃ is equivalent to ⁵⁄₂ x ³⁄₅
- Simplify Before Multiplying (Optional): Notice that we can cancel out a common factor of 5 from the numerator and denominator. This simplifies the calculation to ¹⁄₂ x ³⁄₁
- Multiply: ¹⁄₂ x ³⁄₁ = ³⁄₂
- Convert to a Mixed Number (Optional): ³⁄₂ is equal to 1 ½
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical proficiency. By understanding the concepts of mixed numbers, improper fractions, reciprocals, and simplification, you can confidently tackle various fraction division problems. This comprehensive guide provides a solid foundation, empowering you to solve intricate calculations and apply your knowledge to diverse real-world situations. Remember that practice is key! The more you work with fractions, the more intuitive the process will become. From baking a cake to designing a building, the ability to accurately divide fractions is a valuable skill with far-reaching applications.
Latest Posts
Latest Posts
-
3 Out Of 50 As A Percentage
May 15, 2025
-
How To Find Perimeter Of A Octagon
May 15, 2025
-
0 16666 As A Fraction In Simplest Form
May 15, 2025
-
Circumference Of A 12 Foot Circle
May 15, 2025
-
How To Turn A Number Into A Radical
May 15, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.