1 Is What Percent Of 25
Treneri
May 09, 2025 · 5 min read
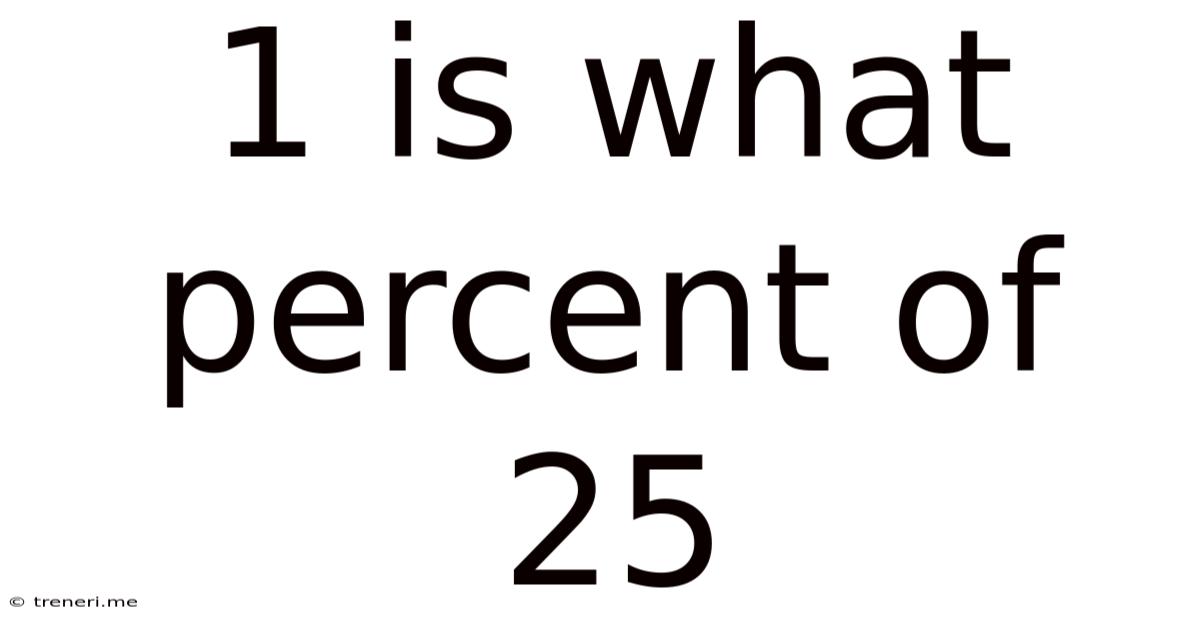
Table of Contents
1 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with widespread applications in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the question, "1 is what percent of 25?", providing a detailed explanation of the calculation process and exploring various methods to solve similar percentage problems. We'll also cover practical examples and discuss the importance of mastering percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are crucial for representing proportions, comparing quantities, and understanding changes or growth rates. They are used extensively in finance, business, science, and everyday life.
Calculating "1 is What Percent of 25?"
To determine what percentage 1 represents of 25, we can employ several methods. The most straightforward approach involves using a simple formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 1
- Whole: 25
Substituting these values into the formula:
(1 / 25) x 100% = 4%
Therefore, 1 is 4% of 25.
Method 1: Using the Formula Directly
This is the most direct and commonly used method. As shown above, simply divide the part (1) by the whole (25) and then multiply the result by 100 to express it as a percentage.
Method 2: Proportion Method
Another way to solve this problem is by setting up a proportion:
1/25 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', cross-multiply:
25x = 100
x = 100/25
x = 4
Therefore, 1 is 4% of 25.
Method 3: Decimal Conversion
We can convert the fraction 1/25 into a decimal by performing the division:
1 ÷ 25 = 0.04
To convert this decimal to a percentage, multiply by 100:
0.04 x 100% = 4%
This confirms that 1 is 4% of 25.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial for numerous real-world applications. Here are some examples:
1. Calculating Discounts and Sales Tax:
Imagine a shirt priced at $25 is on sale for 20% off. To calculate the discount, you'd find 20% of $25:
(20/100) x $25 = $5
The discount is $5, and the final price would be $20. Conversely, calculating sales tax involves finding a percentage of the original price.
2. Analyzing Financial Statements:
Businesses use percentages to analyze financial data, such as profit margins, growth rates, and debt ratios. For example, if a company's net income is $1 million on revenue of $25 million, its profit margin is:
(1/25) x 100% = 4%
This indicates the company's profit margin is 4%.
3. Understanding Statistics and Data Analysis:
Percentages are frequently used in statistics to represent proportions within datasets. For instance, if a survey shows that 1 out of every 25 respondents prefers a particular product, this can be expressed as 4% preference.
4. Calculating Interest Rates:
Interest rates on loans and investments are expressed as percentages. Understanding these percentages is essential for making informed financial decisions.
Beyond the Basics: More Complex Percentage Problems
While the "1 is what percent of 25?" problem is relatively simple, the principles can be applied to more complex scenarios:
Finding the Whole When the Percentage and Part are Known:
Suppose you know that 4% of a certain number is 1. To find the whole number, you can use the formula:
(Part / Percentage) x 100 = Whole
(1 / 4) x 100 = 25
This confirms that 25 is the whole number.
Finding the Part When the Percentage and Whole are Known:
If you know that 4% of 25 is a certain number, you can find the part by:
(Percentage/100) x Whole = Part
(4/100) x 25 = 1
This shows that the part is 1.
Percentage Change Calculations:
Percentage change calculations are used to determine the increase or decrease in a value over time. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying concepts. Here are some tips:
- Practice Regularly: Solve various percentage problems to build your proficiency. Start with simple problems and gradually move towards more complex ones.
- Understand the Formula: Familiarize yourself with the basic percentage formula and its variations. Understanding the underlying logic will help you solve problems more efficiently.
- Use Different Methods: Try different approaches, such as the formula method, the proportion method, and decimal conversion, to find the solution that works best for you.
- Check Your Work: Always verify your calculations to ensure accuracy. A simple mistake can lead to incorrect results.
- Use Online Resources: Numerous online resources, including calculators and tutorials, can help you learn and practice percentage calculations.
Conclusion: The Importance of Percentage Skills
The ability to calculate percentages accurately is a valuable skill with far-reaching implications. From personal finance to professional endeavors, understanding percentages is essential for making informed decisions, analyzing data, and successfully navigating various aspects of daily life. By mastering percentage calculations, you equip yourself with a powerful tool that enhances your problem-solving abilities and improves your overall understanding of numerical data. The simple problem of "1 is what percent of 25?" serves as a foundational stepping stone to a much broader understanding of percentages and their applications. Consistent practice and a clear understanding of the underlying principles will lead to proficiency in this crucial area of mathematics.
Latest Posts
Latest Posts
-
Weight Of 1 Pint Of Water
May 09, 2025
-
Cuanto Es 1 M En Pies
May 09, 2025
-
Finding An Exponential Function Given Two Points
May 09, 2025
-
How Many Minutes Is A Mile Driving
May 09, 2025
-
Greatest Common Factor Of 42 And 48
May 09, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.