1 Is What Percent Of 4
Treneri
May 13, 2025 · 4 min read
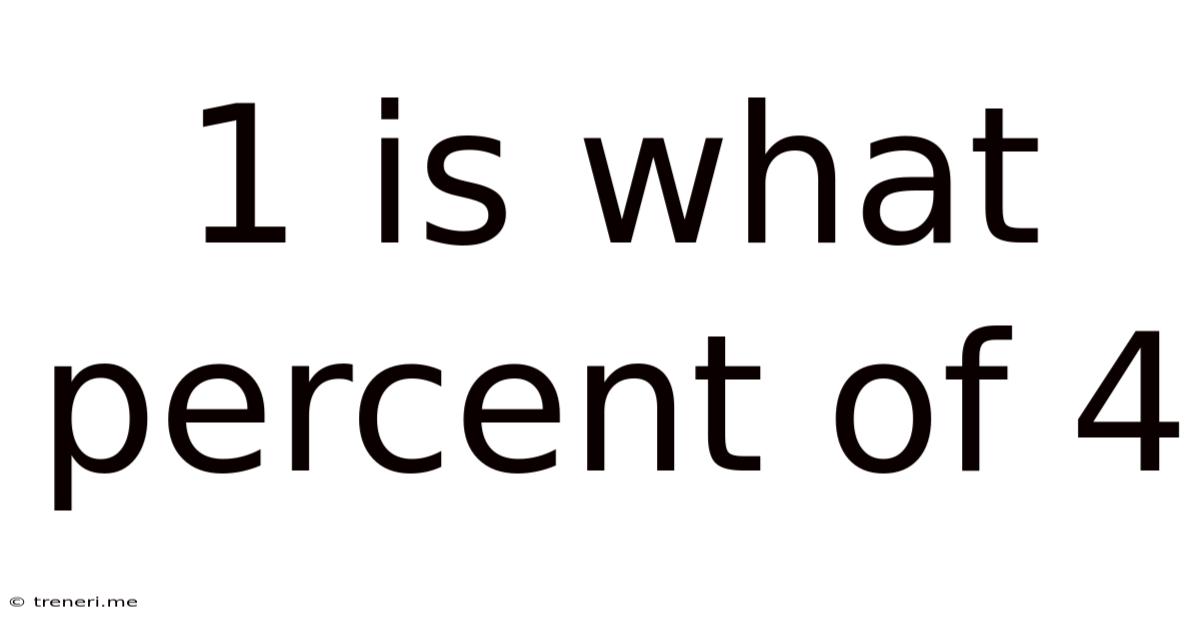
Table of Contents
1 is What Percent of 4? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistics and financial reports. This comprehensive guide delves into the question, "1 is what percent of 4?", providing not just the answer but a thorough explanation of the underlying concepts and practical applications. We'll explore different methods for solving percentage problems and offer valuable tips for mastering this crucial mathematical skill.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental relationship is crucial for solving percentage problems.
Method 1: Using the Percentage Formula
The most direct way to determine what percent 1 is of 4 is by utilizing the standard percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 1 (the number we're comparing)
- Whole: 4 (the total number)
Substituting these values into the formula:
(1 / 4) x 100% = 25%
Therefore, 1 is 25% of 4.
Breaking Down the Calculation
Let's dissect the calculation step-by-step:
-
Division: First, divide the part (1) by the whole (4): 1 / 4 = 0.25
-
Multiplication: Next, multiply the result by 100 to express it as a percentage: 0.25 x 100% = 25%
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
x / 100 = 1 / 4
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
4x = 100
Then, divide both sides by 4:
x = 25
This confirms that 1 is 25% of 4.
Method 3: Using Decimal Equivalents
This method involves converting the fraction to a decimal and then to a percentage.
-
Fraction to Decimal: Convert the fraction 1/4 to a decimal by performing the division: 1 ÷ 4 = 0.25
-
Decimal to Percentage: Multiply the decimal by 100 to obtain the percentage: 0.25 x 100% = 25%
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in numerous real-world scenarios:
1. Retail Discounts:
Imagine a shirt originally priced at $4 is on sale for $1. Using the methods described above, we've already established that the discount is 25%.
2. Tax Calculations:
If a sales tax rate is 6%, and an item costs $4, the tax amount is calculated as (6/100) x $4 = $0.24.
3. Financial Analysis:
Percentage calculations are essential for analyzing financial statements, calculating profit margins, and understanding rates of return on investments. For example, if a business has a profit of $1 on a $4 investment, its profit margin is 25%.
4. Statistical Analysis:
Percentages are frequently used to represent data in charts and graphs, making it easier to visualize and interpret information.
Tips for Mastering Percentage Calculations
-
Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various examples and problems to build your confidence and understanding.
-
Utilize Different Methods: Try different approaches to solve percentage problems. This helps to solidify your understanding and allows you to choose the method that best suits the specific problem.
-
Check Your Work: Always verify your calculations to ensure accuracy.
-
Use Calculators Strategically: Calculators can be helpful, particularly for complex problems, but it's important to understand the underlying concepts to effectively use them.
-
Break Down Complex Problems: If you encounter a challenging percentage problem, try breaking it down into smaller, more manageable steps.
Beyond the Basics: More Complex Percentage Problems
While "1 is what percent of 4?" provides a straightforward illustration, percentage problems can become more intricate. For instance, you might encounter scenarios where you need to calculate percentage increase or decrease, or find a value after applying a percentage change.
These scenarios often require a deeper understanding of the underlying mathematical principles and may involve multiple steps. However, a solid grasp of the fundamental concepts discussed in this article will provide a strong foundation for tackling these more complex challenges.
Conclusion
Understanding how to calculate percentages is a valuable skill with widespread applications. This comprehensive guide has demonstrated various methods for determining the percentage one number represents of another, using the example "1 is what percent of 4?". By understanding these methods and practicing regularly, you'll be well-equipped to handle percentage calculations confidently and efficiently across diverse contexts. Remember to break down complex problems into smaller steps and utilize the methods outlined to arrive at accurate solutions. Mastering percentages opens the door to better comprehension of financial reports, statistical data, and numerous other aspects of daily life.
Latest Posts
Latest Posts
-
Whats The Greatest Common Factor Of 8 And 12
May 13, 2025
-
50 Of 30 Is 15 Of What Number
May 13, 2025
-
Cuantos Son 11 Kilos En Libras
May 13, 2025
-
11 Cups Is How Many Ounces
May 13, 2025
-
60 Days From July 28 2024
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.