1 Is What Percent Of 50
Treneri
May 12, 2025 · 4 min read
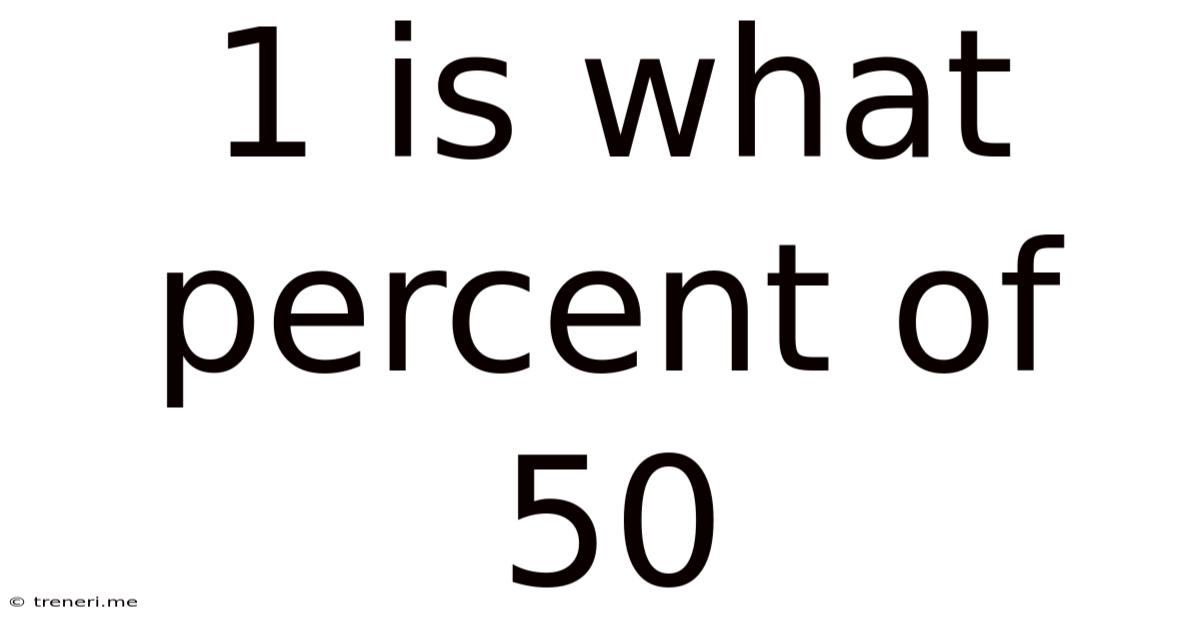
Table of Contents
1 is What Percent of 50? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This comprehensive guide delves into the seemingly simple question, "1 is what percent of 50?", providing a step-by-step explanation, exploring different calculation methods, and offering practical applications to solidify your understanding of percentage calculations.
Understanding the Fundamentals of Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The symbol "%" denotes a percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Key Terms and Concepts
- Part: This represents the smaller quantity you're comparing to the whole. In our example, "1" is the part.
- Whole: This is the larger quantity to which the part is being compared. In our example, "50" is the whole.
- Percentage: This expresses the part as a fraction of the whole, scaled to 100. This is what we need to calculate.
Calculating "1 is What Percent of 50?"
There are several ways to calculate this percentage. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Substituting our values:
(1 / 50) * 100 = Percentage
This simplifies to:
0.02 * 100 = 2%
Therefore, 1 is 2% of 50.
Method 2: Setting up a Proportion
Proportions offer another effective way to solve percentage problems. We can set up a proportion as follows:
1/50 = x/100
Here:
- 1 represents the part.
- 50 represents the whole.
- x represents the unknown percentage we need to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
50x = 100
Divide both sides by 50:
x = 2
Thus, x = 2%, confirming our previous result.
Method 3: Using Decimal Conversion
We can convert the fraction (1/50) into a decimal first and then multiply by 100 to express it as a percentage:
1/50 = 0.02
0.02 * 100 = 2%
This method highlights the direct relationship between decimals and percentages.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in numerous everyday situations. Let's explore some examples:
1. Discount Calculations:
Imagine a store offers a 2% discount on a $50 item. To calculate the discount amount, we would use the same principle:
2% of $50 = (2/100) * $50 = $1
The discount would be $1.
2. Tax Calculations:
If a 2% sales tax is applied to a $50 item, the tax amount would be:
2% of $50 = (2/100) * $50 = $1
The total cost, including tax, would be $51.
3. Grade Calculations:
Suppose you answered 1 out of 50 questions correctly on a test. Your percentage score would be:
(1/50) * 100 = 2%
4. Statistical Analysis:
In data analysis, percentages are used to represent proportions within a larger dataset. For instance, if 1 out of 50 participants in a study responded positively, that would represent 2% of the participants.
5. Financial Applications:
Percentage calculations are fundamental in finance. Calculating interest rates, returns on investments, and understanding financial reports all rely heavily on percentage calculations. For example, if you invest $50 and receive a 2% return, you would earn $1.
Expanding Your Understanding: Working with Larger and Smaller Numbers
The principles discussed above remain consistent regardless of the size of the numbers involved. Whether you're calculating 10 is what percent of 500 or 0.5 is what percent of 25, the same formulas and methods apply. Let's illustrate with an example:
Example: What percent of 500 is 10?
Using the formula: (10 / 500) * 100 = 2%
The result is still 2%, demonstrating the scalability of these calculation methods.
Troubleshooting Common Mistakes
While percentage calculations are relatively straightforward, common mistakes can occur. Here are some to watch out for:
- Incorrect Formula Application: Ensure you correctly substitute the "part" and "whole" values into the formula.
- Decimal Errors: Accuracy in decimal calculations is vital. Double-check your decimal point placement.
- Unit Consistency: Always maintain consistency in units (e.g., dollars, kilograms, etc.).
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is an invaluable skill for everyday life and professional success. By mastering the formulas, methods, and practical applications discussed in this comprehensive guide, you'll be equipped to confidently tackle percentage problems of any size and complexity. Remember, consistent practice and attention to detail are key to achieving proficiency in percentage calculations. From everyday shopping to complex financial analysis, the ability to understand and calculate percentages will serve you well in various aspects of your life. So, next time you encounter a percentage problem, remember the simple yet powerful formula and the various methods discussed here, and confidently solve it.
Latest Posts
Latest Posts
-
How Many Ml In 45 Grams
May 13, 2025
-
How Much Is 500 Feet In Miles
May 13, 2025
-
How To Measure For Wall Mount Tv
May 13, 2025
-
How Much Force Can A Human Exert
May 13, 2025
-
How Many Days Since July 27 2022
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.