1 Raised To The Power Of 5
Treneri
May 13, 2025 · 5 min read
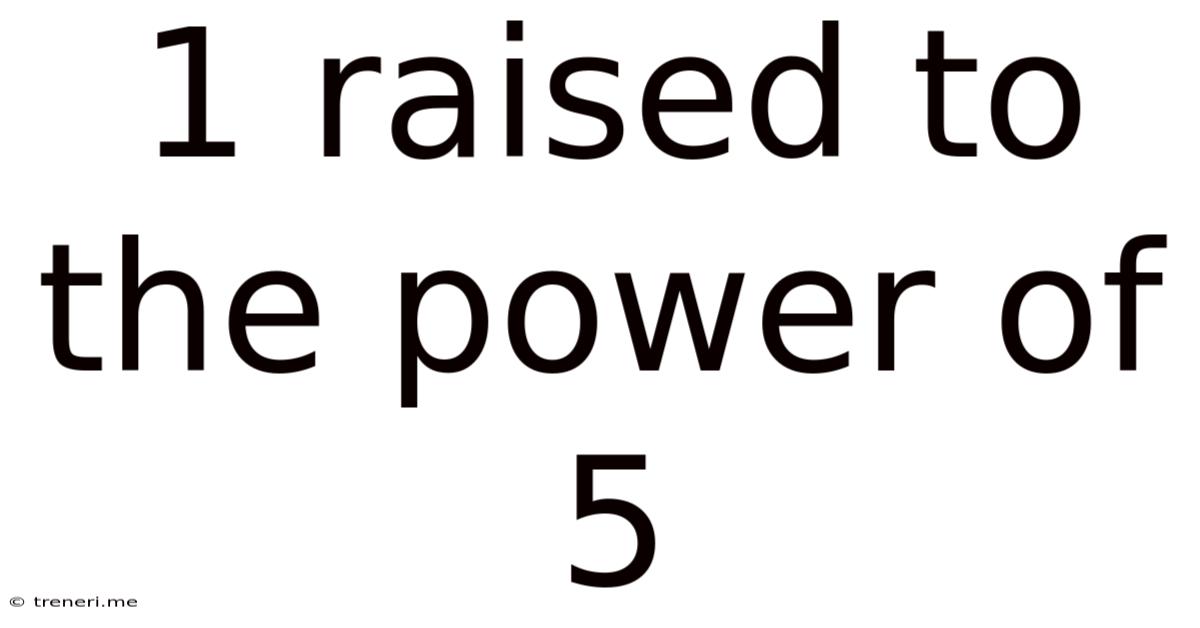
Table of Contents
1 Raised to the Power of 5: A Deep Dive into Exponents and Their Implications
The seemingly simple expression "1 raised to the power of 5," or 1⁵, might appear trivial at first glance. However, exploring this seemingly basic mathematical concept opens a door to understanding fundamental principles of exponents, their properties, and their broader implications within various fields of mathematics and beyond. This exploration will delve into the core concepts, examine related mathematical properties, and discuss the significance of this seemingly simple calculation.
Understanding Exponents
Before diving into the specifics of 1⁵, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the general expression b<sup>n</sup>, 'b' represents the base, and 'n' represents the exponent. Thus, b<sup>n</sup> means 'b' multiplied by itself 'n' times. For instance, 2³ (2 raised to the power of 3) equals 2 x 2 x 2 = 8.
The Significance of the Base Number
The base number plays a crucial role in determining the outcome of exponentiation. Different base numbers, when raised to the same power, yield vastly different results. Consider 2⁵ (32) versus 10⁵ (100,000). The significant difference underscores the impact of the base on the final value. This becomes even more pronounced with larger exponents.
The Uniqueness of the Base Number 1
The number 1 holds a unique position within the realm of exponents. Regardless of the exponent's value, any positive integer power of 1 will always result in 1. This is because multiplying 1 by itself any number of times always yields 1. This is a fundamental property that simplifies many mathematical operations and calculations.
Calculating 1⁵
Now, let's directly address the core topic: 1⁵. Applying the definition of exponents, we can calculate this as:
1⁵ = 1 x 1 x 1 x 1 x 1 = 1
The result, as expected, is 1. This seemingly simple calculation highlights the unique behavior of the number 1 when used as a base in exponential expressions.
Exploring the Properties of Exponents
Understanding the properties of exponents is crucial for manipulating and solving mathematical equations involving powers. Let's explore some key properties and how they relate to 1⁵:
The Zero Exponent Rule
Any non-zero number raised to the power of zero equals 1. This is a crucial rule in algebra and simplifies many expressions. While 1⁰ is consistent with this rule, it's important to note that 0⁰ is undefined.
The Product of Powers Rule
When multiplying two numbers with the same base, you add their exponents. This is represented as: b<sup>m</sup> x b<sup>n</sup> = b<sup>m+n</sup>. This rule can be applied to expressions involving 1, although it doesn't alter the result significantly since the base remains 1.
The Quotient of Powers Rule
When dividing two numbers with the same base, you subtract their exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>m-n</sup>. Again, this applies to 1 as a base but doesn't change the final value which always remains 1.
The Power of a Power Rule
When raising a power to another power, you multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>mn</sup>. This rule also applies to 1 as a base, resulting in 1 raised to the product of the exponents.
Applications and Implications
While 1⁵ might seem insignificant on its own, the concept of raising 1 to any power has far-reaching implications in various mathematical contexts:
Simplification of Complex Equations
In complex algebraic expressions, the property that 1 raised to any power equals 1 often simplifies calculations considerably. This simplification is particularly beneficial when dealing with polynomials, matrices, and other higher-level mathematical constructs.
Identity Elements in Abstract Algebra
In abstract algebra, the number 1 serves as the multiplicative identity element. This means that multiplying any element by 1 leaves the element unchanged. This property extends to exponential operations, where 1 raised to any power maintains its identity as the multiplicative identity.
Probability and Statistics
In probability and statistics, the number 1 often represents certainty or a probability of 100%. Raising 1 to a power doesn't alter this certainty, reflecting the consistent nature of events with 100% probability.
Computer Science and Programming
In computer science and programming, the number 1 plays a fundamental role in Boolean logic and bitwise operations. Raising 1 to a power retains its binary representation, simplifying calculations in various programming contexts.
Beyond the Basics: Exploring More Complex Scenarios
While 1⁵ provides a straightforward calculation, let's consider more complex scenarios involving exponents and the number 1:
Complex Numbers and 1<sup>z</sup>
When dealing with complex numbers, raising 1 to a complex number z (where z = a + bi, where a and b are real numbers and i is the imaginary unit) results in a set of values. Understanding this requires delving into the concept of complex exponentiation and Euler's formula (e<sup>ix</sup> = cos x + i sin x). The solutions are generally complex numbers themselves.
Fractional and Negative Exponents
Raising 1 to a fractional or negative exponent still results in 1. For instance, 1<sup>-2</sup> = 1/(1²) = 1 and 1<sup>1/2</sup> (the square root of 1) equals 1. This further emphasizes the consistent behavior of 1 as a base in exponential expressions.
Limits and Calculus
In calculus, when dealing with limits involving exponents, the behavior of 1 raised to any power remains constant and often simplifies the evaluation of complex limits.
Conclusion: The Unsung Importance of 1⁵
While the calculation of 1⁵ yields a simple result (1), its significance lies within the broader context of exponential properties and their applications across various mathematical disciplines. Understanding the unique behavior of the number 1 as a base in exponential expressions is fundamental to simplifying calculations, mastering algebraic manipulation, and grasping the deeper implications within more complex mathematical frameworks. The seemingly trivial 1⁵ thus serves as a gateway to a more profound appreciation of the power and elegance of mathematics. The consistent outcome reinforces fundamental principles, simplifies complex computations, and highlights the unifying nature of mathematical concepts across different areas of study. From basic arithmetic to advanced calculus, the simplicity of 1 raised to any power belies its significant role in the mathematical landscape.
Latest Posts
Latest Posts
-
What Is The Square Feet Of 10x10
May 14, 2025
-
What Is The Equivalent Fraction For 5 10
May 14, 2025
-
What Is 1 2 3 8 In Fraction Form
May 14, 2025
-
Calories Burned 20 Mile Bike Ride
May 14, 2025
-
How To Find 21 Percent Of A Number
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1 Raised To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.