10 Divided By Square Root Of 2
Treneri
May 15, 2025 · 5 min read
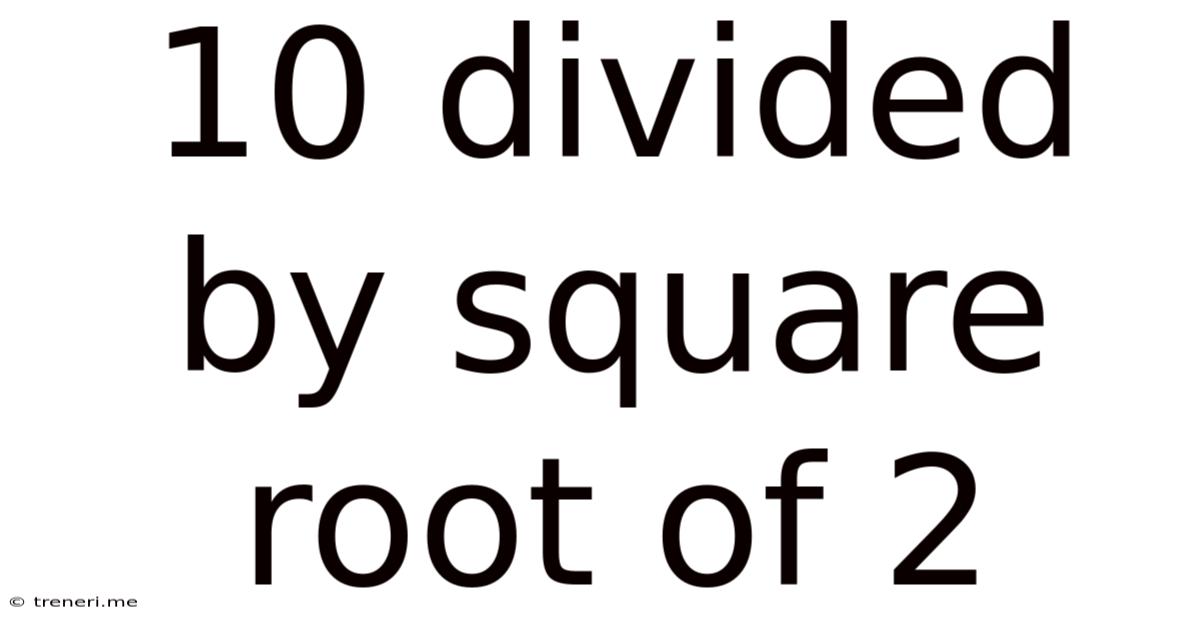
Table of Contents
10 Divided by the Square Root of 2: A Deep Dive into Simplification and Applications
The seemingly simple mathematical expression "10 divided by the square root of 2" (10/√2) presents a rich opportunity to explore fundamental concepts in mathematics, including simplification of radicals, rationalization of denominators, and its applications in various fields. This article delves into the intricacies of this expression, exploring multiple methods of simplification, discussing its geometric interpretations, and showcasing its relevance in practical scenarios.
Understanding the Problem: 10/√2
At its core, the problem asks us to find the quotient when 10 is divided by the square root of 2. This involves working with irrational numbers, which are numbers that cannot be expressed as a simple fraction (a ratio of two integers). The square root of 2 (approximately 1.414) is a classic example of an irrational number. Directly dividing 10 by this approximate value provides an approximate answer, but mathematicians prefer exact solutions whenever possible. This is where the power of mathematical simplification comes into play.
Method 1: Rationalizing the Denominator
The most common approach to simplifying expressions like 10/√2 involves rationalizing the denominator. This process eliminates the radical (square root) from the denominator, resulting in a more manageable and often preferred form. We achieve this by multiplying both the numerator and the denominator by the square root of 2:
(10/√2) * (√2/√2) = (10√2) / (√2 * √2) = (10√2) / 2
This simplifies further to:
5√2
This is the simplified, exact form of 10/√2. It's considered more elegant and easier to work with in further calculations than the original expression.
Method 2: Using the Properties of Square Roots
Another way to approach this simplification involves understanding the properties of square roots. We can rewrite the expression as:
10/√2 = 10 * (1/√2)
Then, we can rationalize the fraction (1/√2) separately:
(1/√2) * (√2/√2) = √2/2
Substituting this back into the original expression gives:
10 * (√2/2) = 10√2 / 2 = 5√2
This method demonstrates the same result but uses a slightly different approach, reinforcing the understanding of square root manipulation.
Method 3: Approximation and Calculation
While the exact form 5√2 is preferable, we can also calculate an approximate value. Using the approximation √2 ≈ 1.414, we have:
10 / 1.414 ≈ 7.071
This approximate value is useful for practical applications where a precise numerical result is needed, but it lacks the elegance and accuracy of the exact form 5√2. It’s important to remember that this is an approximation, and the true value is slightly different.
Geometric Interpretation
The expression 10/√2 has a clear geometric interpretation. Consider a right-angled isosceles triangle with legs of length x. The hypotenuse (the longest side) is given by the Pythagorean theorem: hypotenuse = √(x² + x²) = x√2.
If the hypotenuse of this triangle is 10, then we have:
10 = x√2
Solving for x (the length of the leg) yields:
x = 10/√2 = 5√2
This shows that 5√2 represents the length of the legs in a right-angled isosceles triangle with a hypotenuse of 10. This geometric interpretation provides a visual understanding of the numerical result.
Applications of 10/√2 and Related Concepts
The simplification of expressions involving square roots and the concept of rationalizing the denominator are crucial in many areas of mathematics and science. Here are a few examples:
1. Trigonometry
Trigonometric functions often involve square roots, particularly when dealing with angles other than 30°, 45°, and 60°. Simplifying expressions like 10/√2 is fundamental to solving trigonometric equations and simplifying trigonometric identities.
2. Physics
Many physics problems involve vectors and calculations using the Pythagorean theorem. Dealing with irrational numbers stemming from square roots is common when calculating distances, velocities, or forces in two or three dimensions.
3. Engineering
Engineers routinely encounter calculations involving square roots in areas such as structural analysis, electrical engineering, and mechanical design. The ability to simplify such expressions efficiently is essential for accurate and efficient problem-solving.
4. Computer Graphics
In computer graphics, calculations using vectors and matrices frequently involve square roots and rationalization of denominators for tasks such as 3D rendering, transformations, and lighting calculations.
5. Calculus
The simplification of radical expressions is crucial in calculus, specifically when dealing with derivatives and integrals. Often, simplifying expressions before differentiation or integration makes the process significantly easier.
Beyond 10/√2: Generalizing the Concept
The method used to simplify 10/√2 can be generalized to any expression of the form a/√b, where 'a' and 'b' are constants. The process of rationalizing the denominator remains the same: multiply both the numerator and denominator by √b. This results in:
(a/√b) * (√b/√b) = a√b / b
This general formula highlights the underlying mathematical principle at play and allows for the efficient simplification of a broader range of expressions.
Conclusion: The Importance of Mathematical Precision
This in-depth analysis of the expression 10/√2 demonstrates the importance of simplifying mathematical expressions to their most elegant and efficient forms. While an approximate value can suffice in some practical contexts, the exact form, 5√2, offers greater accuracy and clarity. The methods explored—rationalizing the denominator, applying square root properties, and employing a geometric interpretation—highlight the versatility and interconnectedness of various mathematical concepts. The ability to simplify expressions like 10/√2 is a foundational skill with widespread applications in numerous fields, showcasing the power and beauty of mathematical precision. Understanding these methods not only enhances problem-solving skills but also deepens one's appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
What Percent Is 12 Of 36
May 15, 2025
-
Circumference Of A 3 Inch Circle
May 15, 2025
-
43 Rounded To The Nearest Hundred
May 15, 2025
-
How Many Kilocalories Are In One Gram Of Fat
May 15, 2025
-
What Grade Is 4 Out Of 6
May 15, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.