10 Is What Percent Of 30
Treneri
May 10, 2025 · 4 min read
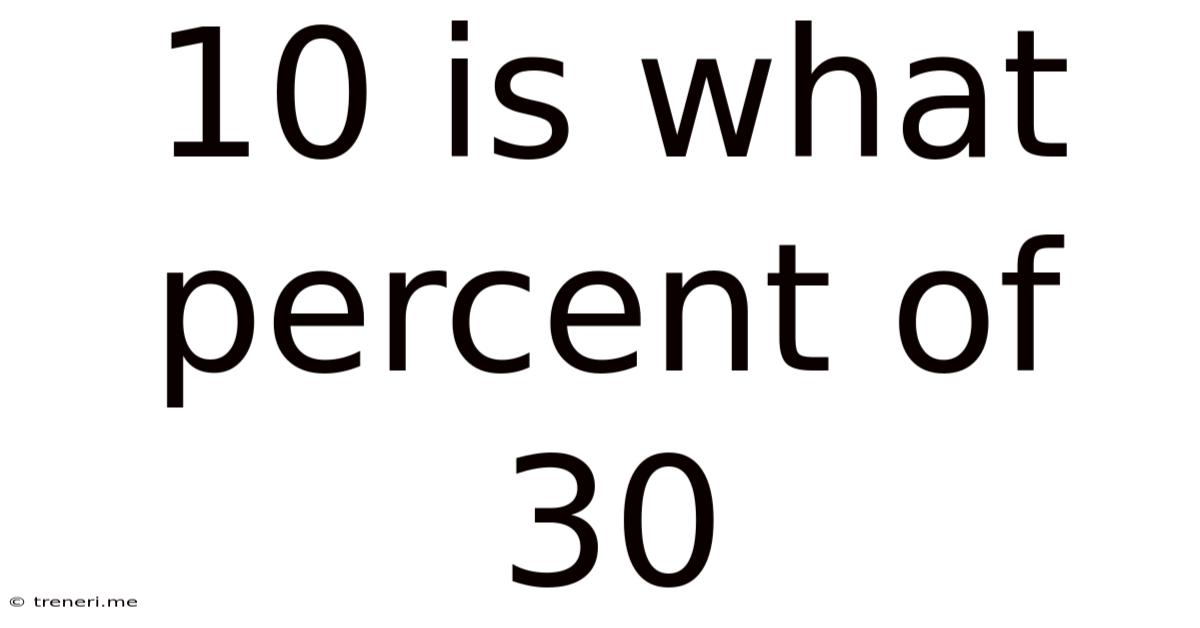
Table of Contents
10 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and tax rates to analyzing data and understanding financial reports. This article delves deep into the question, "10 is what percent of 30?", providing a detailed explanation of the calculation, different approaches to solving the problem, and practical applications to help you master percentage calculations.
Understanding Percentages
Before we dive into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Terms:
- Part: The value you're comparing to the whole. In our case, the part is 10.
- Whole: The total value to which the part is being compared. In our case, the whole is 30.
- Percentage: The ratio of the part to the whole, expressed as a fraction of 100.
Method 1: Using the Formula
The most straightforward way to determine what percentage 10 is of 30 is to use the standard percentage formula:
(Part / Whole) x 100% = Percentage
Substituting our values:
(10 / 30) x 100% = Percentage
This simplifies to:
(1/3) x 100% = 33.333...%
Therefore, 10 is approximately 33.33% of 30. The recurring decimal indicates that the percentage is a repeating decimal. In practical applications, you might round this to 33.3% or 33%. The level of precision depends on the context of your calculation.
Method 2: Using Proportions
Another effective method involves setting up a proportion. We can express the problem as:
10/30 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
30x = 1000
Then divide both sides by 30:
x = 1000/30 = 33.333...
Therefore, 'x' is approximately 33.33%. This method provides a clear visual representation of the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
This method involves first converting the fraction to a decimal, and then multiplying by 100%.
- Convert the fraction: 10/30 simplifies to 1/3.
- Convert the fraction to a decimal: 1/3 = 0.333...
- Convert the decimal to a percentage: 0.333... x 100% = 33.333...%
This method is especially useful when working with a calculator, as it allows for a step-by-step conversion, reducing the chance of errors.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in many everyday situations, including:
1. Finance and Budgeting:
- Calculating discounts: If a product is discounted by 20%, you can easily calculate the final price.
- Determining tax rates: Understanding sales tax percentages allows you to accurately calculate the final cost of purchases.
- Analyzing investment returns: Percentages are essential for tracking the growth or loss of investments.
- Calculating interest rates: Interest on loans and savings accounts is expressed as a percentage.
2. Data Analysis and Statistics:
- Interpreting survey results: Percentages are used extensively to represent data from surveys and polls.
- Analyzing performance metrics: KPIs (Key Performance Indicators) are often expressed as percentages to track progress.
- Creating charts and graphs: Percentages are visually presented in charts and graphs to communicate data effectively.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant often involves percentage calculations.
- Understanding sales and promotions: Recognizing discounts and promotions requires understanding percentages.
- Comparing prices: Comparing the price of products with different quantities often involves calculating unit prices expressed as percentages.
Tips and Tricks for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use a calculator: For more complex calculations, a calculator can save time and reduce errors.
- Master the formula: Understand the core formula (Part/Whole x 100%) thoroughly.
- Break down complex problems: If you're faced with a challenging percentage problem, break it down into smaller, simpler steps.
- Learn shortcuts: There are several calculation shortcuts that can speed up your work. For example, 10% of a number is easily found by dividing by 10.
Conclusion:
The question "10 is what percent of 30?" is readily solved using several methods. We've covered three primary methods: using the standard formula, proportions, and decimal conversion. All approaches consistently demonstrate that 10 is approximately 33.33% of 30. Understanding these calculations is not just important for passing math tests; it's a vital skill applicable in various everyday scenarios, empowering you to make informed decisions and confidently navigate the quantitative aspects of life. By mastering these techniques and practicing regularly, you can build a strong foundation in percentage calculations, enhancing your problem-solving abilities and confidence in tackling various numerical challenges. Remember to always consider the level of precision required for your specific situation when rounding your results.
Latest Posts
Latest Posts
-
Find The Value Of X In An Equilateral Triangle
May 10, 2025
-
81 Months Is How Many Years
May 10, 2025
-
Cuanto Es 16 Onzas En Litros
May 10, 2025
-
What Is A Vertice Of A Triangle
May 10, 2025
-
1 3 1 12 As A Fraction
May 10, 2025
Related Post
Thank you for visiting our website which covers about 10 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.