10 Out Of 16 In Percentage
Treneri
May 14, 2025 · 5 min read
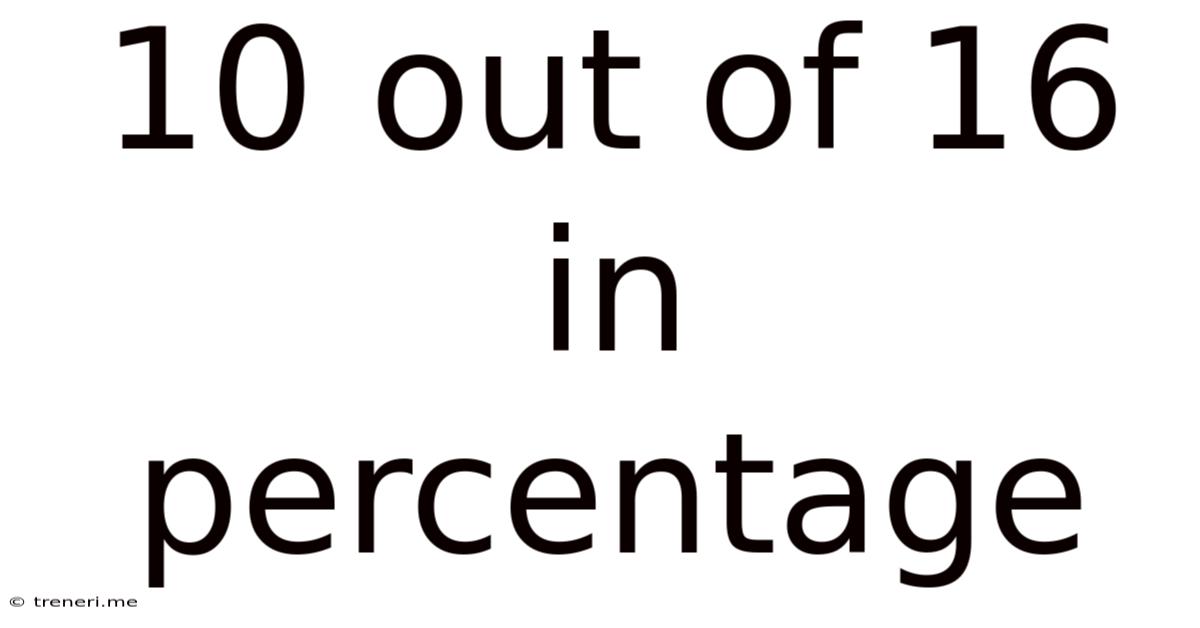
Table of Contents
10 Out of 16: Understanding Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various fields, from academic assessments to financial analysis. Understanding how to express a fraction as a percentage, especially in scenarios like "10 out of 16," is crucial for interpreting data and making informed decisions. This comprehensive guide will explore how to calculate 10 out of 16 as a percentage, delve into the underlying mathematical principles, and demonstrate its practical applications across different domains.
Calculating 10 Out of 16 as a Percentage
The phrase "10 out of 16" represents a fraction where 10 is the part and 16 is the whole. To express this as a percentage, we need to convert this fraction into a percentage. The formula for calculating a percentage is:
(Part / Whole) * 100%
In this case:
(10 / 16) * 100%
-
Divide the part by the whole: 10 ÷ 16 = 0.625
-
Multiply the result by 100: 0.625 * 100 = 62.5
Therefore, 10 out of 16 is 62.5%.
Understanding the Fundamentals: Fractions, Decimals, and Percentages
To fully grasp percentage calculations, it's essential to understand the relationships between fractions, decimals, and percentages. These three represent different ways of expressing the same numerical value.
-
Fraction: Represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). In our example, 10/16 is the fraction.
-
Decimal: Represents a number in base-10 notation, using a decimal point to separate the whole number part from the fractional part. 10/16 is equivalent to the decimal 0.625.
-
Percentage: Represents a fraction or decimal as a portion of 100, denoted by the symbol %. 0.625 is equivalent to 62.5%.
The conversion between these three forms is straightforward:
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Percentage: Multiply the decimal by 100 and add the % symbol.
- Percentage to Decimal: Divide the percentage by 100.
- Percentage to Fraction: Write the percentage as a fraction with 100 as the denominator, then simplify the fraction.
Practical Applications of Percentage Calculations: Real-World Examples
Percentage calculations are ubiquitous, appearing in diverse contexts:
1. Academic Performance:
Imagine a student scored 10 out of 16 on a quiz. Knowing that this equates to 62.5% helps assess their performance relative to the total possible marks. This allows teachers to track student progress and identify areas needing improvement.
2. Financial Analysis:
In finance, percentages are fundamental. For example, calculating the interest rate on a loan, understanding the return on investment (ROI), or analyzing changes in stock prices all involve percentage calculations. If a company's profits increased from 16 million to 26 million, the percentage increase is calculated similarly: (26-16)/16 * 100% = 62.5%.
3. Sales and Discounts:
Retailers frequently use percentages to advertise discounts. A "62.5% off" sale indicates a significant price reduction. Calculating the final price after the discount requires understanding percentages.
4. Surveys and Statistics:
Statistical data is often presented as percentages. For instance, survey results might show that 62.5% of respondents favor a particular policy. Understanding these percentages is crucial for interpreting public opinion and making informed decisions based on the data.
5. Scientific Research:
In scientific research, percentages are used to express experimental results. For example, if an experiment shows a 62.5% success rate, this provides valuable insight into the effectiveness of the process or treatment.
6. Sports Statistics:
In sports, percentages are essential for tracking team and player performance. A basketball player's field goal percentage, for instance, is calculated by dividing the number of successful shots by the total number of attempts and multiplying by 100%.
Beyond the Basics: Advanced Percentage Calculations
While calculating 10 out of 16 as a percentage is relatively straightforward, more complex scenarios may require additional calculations. These include:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%
-
Percentage Points: This represents the absolute difference between two percentages, not a percentage change. For example, an increase from 10% to 16% is a 6 percentage point increase, but a 60% increase based on 10% ([(16-10)/10]*100%).
-
Compound Interest: Interest calculated on both the principal amount and accumulated interest from previous periods. This involves iterative percentage calculations.
-
Percentage of a Percentage: Calculating a percentage of another percentage, such as finding 20% of 62.5%. This involves multiplying the two percentages.
Tips for Accurate Percentage Calculations
To ensure accuracy in percentage calculations:
- Double-check your work: Carefully review your calculations to avoid errors.
- Use a calculator: For more complex calculations, use a calculator to increase accuracy and speed.
- Understand the context: Clearly identify the part and the whole before beginning the calculation.
- Round appropriately: Consider the context when rounding your final answer. In some instances, rounding to the nearest whole number is appropriate, while in others, more decimal places are needed for precision.
Conclusion: Mastering Percentages for Success
Understanding how to calculate percentages, particularly in scenarios like "10 out of 16," is an essential life skill. From academic settings to professional environments, the ability to interpret and utilize percentages effectively is crucial for making informed decisions, analyzing data, and solving problems. By mastering the fundamentals and exploring advanced applications, individuals can enhance their analytical capabilities and navigate various aspects of life with greater confidence and competence. The ability to accurately and efficiently calculate percentages opens doors to a deeper understanding of the world around us, empowering us to make more informed choices in our personal and professional lives. Remember to practice regularly to build fluency and accuracy in your percentage calculations.
Latest Posts
Latest Posts
-
24 Inches By 24 Inches In Square Feet
May 14, 2025
-
1 2 Cubic Yard To Square Feet
May 14, 2025
-
How Many Years Is 125 Months
May 14, 2025
-
Subtract The Quotient Of 70 Divided By 2 From 60
May 14, 2025
-
How Much Hours Is 100 Days
May 14, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 16 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.