10 Times The Square Root Of 2
Treneri
May 07, 2025 · 5 min read
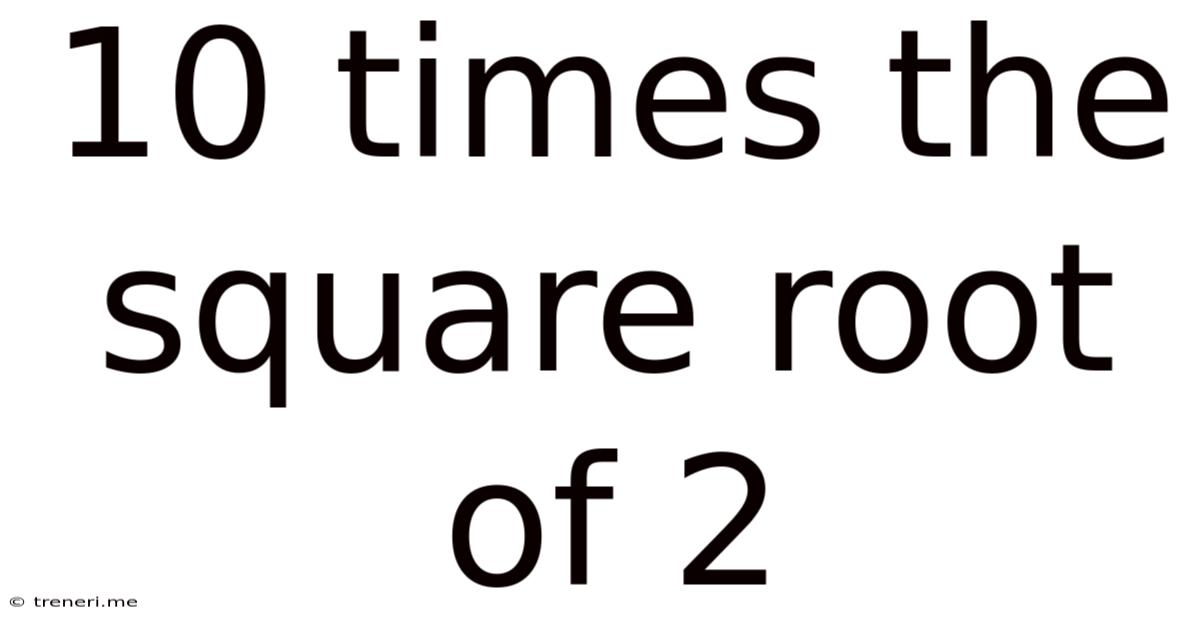
Table of Contents
10 Times the Square Root of 2: Exploring a Mathematical Constant
The seemingly simple expression "10 times the square root of 2" (often written as 10√2) unveils a fascinating journey into the world of mathematics, touching upon various concepts and applications. While it might appear straightforward at first glance, delving deeper reveals its significance in geometry, trigonometry, physics, and even computer programming. This article will explore this mathematical constant in detail, examining its properties, applications, and historical context.
Understanding the Square Root of 2 (√2)
Before diving into 10√2, let's establish a solid understanding of its foundational element: the square root of 2. This irrational number, approximately equal to 1.41421356, represents the positive number that, when multiplied by itself, equals 2. Its irrationality means it cannot be expressed as a simple fraction (a ratio of two integers). This characteristic has intrigued mathematicians for centuries.
The discovery of the square root of 2 is often credited to the Pythagorean school of ancient Greece. Legend states that Hippasus, a Pythagorean, was possibly even banished or killed for revealing this irrational number, which challenged their belief in the absolute dominance of rational numbers. This discovery marked a significant turning point in the history of mathematics, demonstrating the existence of numbers beyond the rational realm.
The Pythagorean Theorem and √2
The square root of 2 arises naturally from the Pythagorean theorem, a cornerstone of geometry. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs).
Consider a right-angled triangle with legs of length 1. By the Pythagorean theorem:
Hypotenuse² = 1² + 1² = 2
Therefore, the hypotenuse has a length of √2. This simple geometric interpretation underscores the fundamental nature of this irrational number and its inherent connection to spatial relationships.
Exploring 10√2: Properties and Calculations
Now, let's focus on the expression 10√2, which is simply 10 multiplied by the square root of 2. This results in an approximate value of 14.1421356. While it's an irrational number like √2, it shares several crucial properties:
-
Irrationality: As a multiple of an irrational number, 10√2 remains irrational. It cannot be expressed as a fraction of two integers.
-
Approximation: While we can't represent 10√2 exactly as a decimal, we can use approximations to a desired level of accuracy. This is often necessary in practical applications where precise calculations might be computationally expensive or impractical.
-
Geometric Significance: Similar to √2, 10√2 has geometric interpretations. For example, it could represent the length of the hypotenuse of a right-angled triangle with legs of length approximately 7.071 (since 7.071² + 7.071² ≈ 100, and √100 = 10).
Calculations Involving 10√2
Calculating with 10√2 often involves using approximations. Standard calculators provide a reasonable approximation. However, for high-precision calculations, more sophisticated methods are employed. For instance, numerical analysis techniques can be used to calculate 10√2 to an arbitrary number of decimal places.
Moreover, the number can be manipulated algebraically. For example, we can express it as √200. This alternate representation can be helpful in certain mathematical operations and simplifications. Understanding these different representations allows for greater flexibility in problem-solving.
Applications of 10√2 and Related Numbers
The constant 10√2, and its related numbers (multiples of √2), find numerous applications across diverse fields:
Geometry and Trigonometry
-
Calculating Diagonal Lengths: In squares and other geometric shapes, 10√2 could represent the length of diagonals. For instance, a square with sides of length 7.071 (approximately 10/√2 or 5√2) would have a diagonal of approximately 10.
-
Trigonometric Functions: The number appears implicitly in various trigonometric calculations, especially those involving angles of 45 degrees. This is due to the inherent relationship between the Pythagorean theorem and trigonometric functions.
Physics and Engineering
-
Vector Calculations: In physics, vectors are used to represent quantities with both magnitude and direction. 10√2 could represent the magnitude of a vector, requiring vector calculations.
-
Mechanical Design: In designing mechanical structures, calculations involving √2 often appear in determining dimensions, stress analysis, and structural integrity.
-
Electrical Engineering: The constant can arise in calculations related to AC circuits, impedance, and phase angles.
Computer Programming and Algorithm Design
-
Computational Geometry: 10√2 and similar irrational numbers are commonly encountered in algorithms used for computer graphics, geometric modeling, and simulation.
-
Numerical Analysis: Approximations of 10√2 are frequently used in numerical methods for solving equations and approximations.
Historical Context and Mathematical Significance
The number 10√2, while not as historically renowned as π or e, represents a fundamental concept within mathematics. Its origins are intertwined with the historical struggle to understand irrational numbers. The discovery and acceptance of irrational numbers fundamentally changed our understanding of the number system and paved the way for more advanced mathematical concepts.
The exploration of 10√2 also highlights the importance of approximation methods in mathematics. While it's an irrational number, its approximate values are readily used in diverse practical applications where precise calculations might be impossible or computationally impractical.
Conclusion: The Ubiquity of 10√2 and Related Constants
In summary, while the expression "10 times the square root of 2" might seem simple, its significance extends far beyond its initial appearance. Its roots lie in fundamental mathematical concepts like the Pythagorean theorem and irrational numbers. Its applications range across diverse fields, from geometry and trigonometry to physics, engineering, and computer programming.
By understanding the properties and applications of 10√2, we gain a deeper appreciation for the interconnectedness of mathematical concepts and their profound influence on our understanding of the world around us. The constant serves as a reminder of the power of seemingly simple mathematical expressions and their surprisingly vast implications. Further exploration into irrational numbers and their various properties would reveal even more fascinating applications and connections within the wider mathematical landscape. The journey of understanding numbers like 10√2 underscores the beauty and intricate elegance inherent in mathematical study.
Latest Posts
Latest Posts
-
How Many Gallons In 21 Foot Round Pool
May 11, 2025
-
Cuanto Es 72 Onzas En Litros
May 11, 2025
-
How Many Miles Is 3500 Kilometers
May 11, 2025
-
What Is 113 Minutes In Hours
May 11, 2025
-
60 Days Before September 8 2024
May 11, 2025
Related Post
Thank you for visiting our website which covers about 10 Times The Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.