10 To The Negative 6th Power
Treneri
Apr 06, 2025 · 5 min read
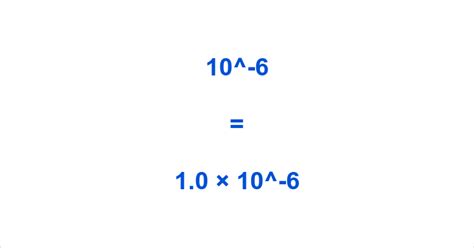
Table of Contents
Decoding 10 to the Negative 6th Power: A Deep Dive into Microworlds
Understanding scientific notation is crucial for navigating the vast scales of the universe, from the incredibly small to the astronomically large. This article delves deep into one specific and frequently encountered exponent: 10 to the negative 6th power, also written as 10<sup>-6</sup> or simply 10⁻⁶. We'll explore its meaning, practical applications, and its significance in various scientific fields.
What Does 10⁻⁶ Mean?
At its core, 10⁻⁶ represents a decimal fraction. Negative exponents in scientific notation indicate reciprocals. Therefore, 10⁻⁶ is the reciprocal of 10⁶ (10 to the power of 6), which is 1,000,000 (one million). This means:
10⁻⁶ = 1/10⁶ = 1/1,000,000 = 0.000001
This value, one-millionth, is a fundamental unit in many scientific measurements, representing a small but significant scale in various contexts.
The Significance of the Micro-Scale
The significance of 10⁻⁶ lies in its ability to represent incredibly small quantities. It allows scientists to express measurements concisely and accurately, avoiding cumbersome decimal notations. This is especially crucial when dealing with microscopic phenomena, where precision is paramount.
Practical Applications in Science and Engineering:
-
Micrometers (µm): The micrometer, often denoted as µm (or micron), is a unit of length equal to 10⁻⁶ meters. This unit is extensively used in microscopy, materials science, and nanotechnology. Imagine measuring the width of a human hair – it's typically around 50-100 µm. Many biological cells are also measured in this range. Understanding 10⁻⁶ is fundamental to grasping the scale of these tiny structures.
-
Microseconds (µs): Similarly, the microsecond (µs) represents 10⁻⁶ seconds. This unit is essential in electronics and high-speed signal processing, allowing for precise timing measurements in rapid-fire circuits and processes. Fast-paced digital signals operate within these tiny time intervals.
-
Micrograms (µg): Mass measurement is also affected by this scale. The microgram (µg) is equal to 10⁻⁶ grams. This unit finds usage in analytical chemistry, where measuring minute amounts of substances is critical. Pharmaceuticals, for example, often deal with substances at this scale.
-
Electrical Engineering: The concept of 10⁻⁶ permeates electrical engineering, often representing small capacitances, inductances, or resistances. Understanding this scale is crucial for designing and analyzing circuits accurately.
-
Fluid Dynamics: Understanding the micro-scale is vital in studying fluid flow. The movement of fluids at a microscopic level, influenced by factors like viscosity and surface tension, is highly relevant in areas like microfluidics.
10⁻⁶ in the Context of Larger Units:
It's instructive to consider how 10⁻⁶ relates to larger units of measurement:
-
Millimeters (mm): 1 mm = 10⁻³ m. There are 1000 µm in 1 mm. This highlights the relationship between different metric prefixes.
-
Nanometers (nm): 1 nm = 10⁻⁹ m. There are 1000 nm in 1 µm. This highlights the transition from the micro-scale to the nanoscale.
-
Kilometers (km): 1 km = 10³ m. There are 10⁹ µm in 1 km, emphasizing the vast difference between these units.
By understanding these relationships, we can easily convert between different units of measurement and grasp the relative sizes of various phenomena.
Beyond the Scientific Realm:
While the primary application of 10⁻⁶ lies in science and engineering, its relevance extends to everyday life, although perhaps less directly. For example:
-
Probability and Statistics: Extremely unlikely events might have probabilities expressed using exponents like 10⁻⁶, representing a 1 in a million chance.
-
Data Analysis: In large datasets, small proportions or anomalies might be expressed using this notation.
-
Finance: Incredibly small changes in financial markets can be represented with the same precision, influencing trading strategies and risk assessments.
Mastering Scientific Notation: Tips and Tricks
Scientific notation, while powerful, can seem daunting at first. Here are some tips to master it:
-
Understand the Base: The base, 10 in our case, dictates the magnitude of the number.
-
Focus on the Exponent: The exponent tells you how many places to move the decimal point. A positive exponent shifts the decimal point to the right, while a negative exponent shifts it to the left.
-
Practice Conversions: Convert numbers between standard form and scientific notation frequently to solidify your understanding.
-
Utilize Online Calculators: Don't hesitate to employ online calculators to double-check your calculations and build confidence.
-
Break Down Complex Problems: If faced with complex equations, break them down into smaller, manageable parts to avoid confusion.
Further Exploration: Related Concepts
Understanding 10⁻⁶ naturally leads to exploring related concepts within the broader context of scientific measurement and notation:
-
Metric Prefixes: Familiarizing yourself with the complete set of metric prefixes (kilo, milli, micro, nano, pico, etc.) is essential for accurate scientific communication.
-
Significant Figures: Understanding significant figures helps communicate the precision of measurements, ensuring that reported values reflect the actual accuracy of the data.
-
Dimensional Analysis: This technique helps verify the correctness of calculations by analyzing the units of measurements involved.
-
Orders of Magnitude: Comparing values using orders of magnitude provides a quick and effective way to understand their relative sizes.
Conclusion: The Ubiquity of 10⁻⁶
10⁻⁶, or one-millionth, is far more than just a numerical value; it's a key to understanding the intricate workings of the microworld. From microscopic biological structures to high-speed electronic circuits, this exponent plays a vital role in countless scientific and engineering applications. Mastering its meaning and applications is crucial for anyone seeking a deeper understanding of science, technology, and the world around us. Its concise representation and consistent application in scientific notation make it a fundamental tool for clear and precise communication within the scientific community and beyond. By understanding this seemingly small number, we unlock the door to a universe of microscopic wonders.
Latest Posts
Latest Posts
-
How Do You Find The Lateral Area Of A Cone
Apr 07, 2025
-
Cuanto Es Un Gramo En Cucharadas
Apr 07, 2025
-
31 Kilometers Is How Many Miles
Apr 07, 2025
-
How Long Is 4960 Weeks In Years
Apr 07, 2025
-
How To Calculate The Focal Length
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 10 To The Negative 6th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.