100 000 As A Power Of 10
Treneri
May 14, 2025 · 5 min read
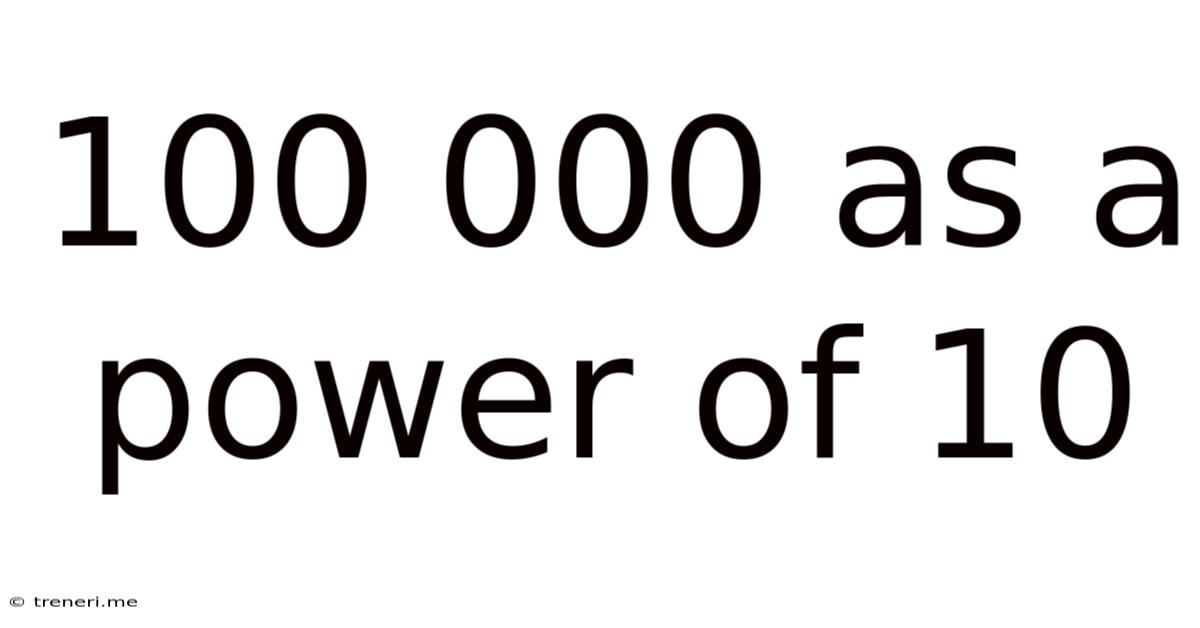
Table of Contents
100,000 as a Power of 10: Exploring Scientific Notation and its Applications
The number 100,000, while seemingly straightforward, holds significant importance in mathematics and various scientific fields. Understanding its representation as a power of 10 is crucial for grasping concepts like scientific notation, orders of magnitude, and the vast scales encountered in science and engineering. This article delves into the representation of 100,000 as a power of 10, explores its applications, and highlights the importance of scientific notation in simplifying and understanding very large or very small numbers.
Understanding Scientific Notation
Scientific notation is a standardized way of writing numbers that are too large or too small to be conveniently written in decimal form. It expresses numbers in the form of a coefficient multiplied by a power of 10. The coefficient is always a number between 1 and 10 (but not including 10), and the power of 10 indicates the order of magnitude.
For instance, the number 100,000 can be written in scientific notation as:
1 x 10<sup>5</sup>
Here, 1 is the coefficient, and 10<sup>5</sup> represents 10 multiplied by itself five times (10 x 10 x 10 x 10 x 10 = 100,000). The exponent, 5, signifies that the decimal point in the coefficient should be moved five places to the right to obtain the standard decimal representation.
Why Use Scientific Notation?
Scientific notation offers several advantages:
-
Compactness: It significantly reduces the length of very large or very small numbers, making them easier to write and manipulate. Imagine writing out the number of atoms in a gram of hydrogen—scientific notation makes this manageable.
-
Clarity: It enhances readability and avoids the ambiguity associated with strings of zeros. It instantly conveys the magnitude of the number.
-
Calculations: Scientific notation simplifies calculations involving very large or small numbers. Multiplication and division become easier when dealing with powers of 10. Adding and subtracting requires adjusting exponents to align decimal places, but it's still significantly more efficient than working with long decimal numbers.
-
Consistency: It provides a uniform standard for representing numbers across various scientific disciplines, facilitating communication and data analysis.
100,000 in Different Contexts
The number 100,000 holds different meanings depending on the context:
Financial Context:
- A significant sum: 100,000 represents a substantial amount of money in many contexts, especially for individuals or small businesses. It could represent a down payment on a house, a significant investment, or a year's worth of savings. Understanding this number’s magnitude is crucial for financial planning and decision-making.
Population Context:
- A sizeable community: 100,000 people represent a sizable city or town. Understanding population numbers allows for better resource allocation, urban planning, and infrastructure development.
Scientific Context:
-
Orders of Magnitude: In scientific contexts, 100,000 often serves as a benchmark for understanding orders of magnitude. For example, the distance between the Earth and the Sun is vastly larger than 100,000 kilometers; the size of certain molecules are vastly smaller. Understanding orders of magnitude allows scientists to compare quantities across vastly different scales.
-
Data Analysis: Large datasets frequently involve numbers in the range of 100,000 or even millions. Scientific notation is essential for managing, analyzing, and visualizing such data effectively. Statistical calculations become far more efficient with this method.
Practical Applications of 100,000 as a Power of 10
The representation of 100,000 as 10<sup>5</sup> has numerous practical applications:
-
Computer Science: Computer memory is often measured in bytes, kilobytes (KB), megabytes (MB), and gigabytes (GB). Understanding powers of 10 allows us to easily convert between these units, as 1 KB = 1024 bytes (approximately 10<sup>3</sup> bytes), 1 MB = 1024 KB (approximately 10<sup>6</sup> bytes), and so on.
-
Engineering: Engineers use scientific notation to represent large quantities, such as the amount of material needed for a large-scale construction project or the power output of a power plant. Accuracy is paramount, and the clarity of scientific notation proves invaluable.
-
Astronomy: In astronomy, distances between celestial bodies are often expressed in scientific notation. Understanding these vast distances helps us comprehend the scale of the universe. For instance, light-years are commonly employed, involving multiples of 10<sup>13</sup> kilometers and even larger numbers.
-
Physics: Physics deals with both incredibly large and incredibly small quantities. Atomic scales, for instance, involve units such as nanometers (10<sup>-9</sup> meters), while cosmological scales use light-years (10<sup>16</sup> meters). Scientific notation is essential for handling this vast range of scales.
Extending the Concept: Powers of 10 and Logarithmic Scales
The concept of representing numbers as powers of 10 naturally extends to logarithmic scales. Logarithmic scales compress large ranges of numbers into a smaller, more manageable scale. They are frequently used when dealing with data that spans many orders of magnitude, such as:
-
The Richter scale for earthquake magnitude: Each whole number increase represents a tenfold increase in amplitude.
-
The pH scale for acidity: A change of one pH unit represents a tenfold change in hydrogen ion concentration.
-
Decibel scales for sound intensity: Each 10 dB increase represents a tenfold increase in sound intensity.
Understanding powers of 10 and their application in logarithmic scales is critical for comprehending these measurements and their implications.
Conclusion: The Significance of 100,000 and Scientific Notation
The number 100,000, when expressed as 1 x 10<sup>5</sup>, is more than just a numerical representation. It’s a keystone in understanding scientific notation, orders of magnitude, and the vast scales we encounter in various fields. The ability to easily manipulate large and small numbers through scientific notation is indispensable for clear communication, efficient calculations, and a deeper understanding of the quantitative world around us. From finance and population studies to physics and astronomy, the application of powers of 10 provides a common language and a powerful tool for navigating the complexities of data and phenomena at all scales. Mastering this concept unlocks a deeper appreciation for the quantitative nature of our world and equips individuals with the necessary tools for success in STEM fields and beyond. The seemingly simple number 100,000, therefore, represents a gateway to a much wider understanding of scientific principles and their practical applications.
Latest Posts
Latest Posts
-
86 Grams Is How Many Ounces
May 14, 2025
-
What Is The Slope Of The Equation Mc016 1 Jpg
May 14, 2025
-
Cuantos Bloques Lleva Una Pared De 4 Metros
May 14, 2025
-
What Is 10 Ml In Oz
May 14, 2025
-
11 Ounces Equals How Many Cups
May 14, 2025
Related Post
Thank you for visiting our website which covers about 100 000 As A Power Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.