100 Decreased By A Number K
Treneri
May 10, 2025 · 5 min read
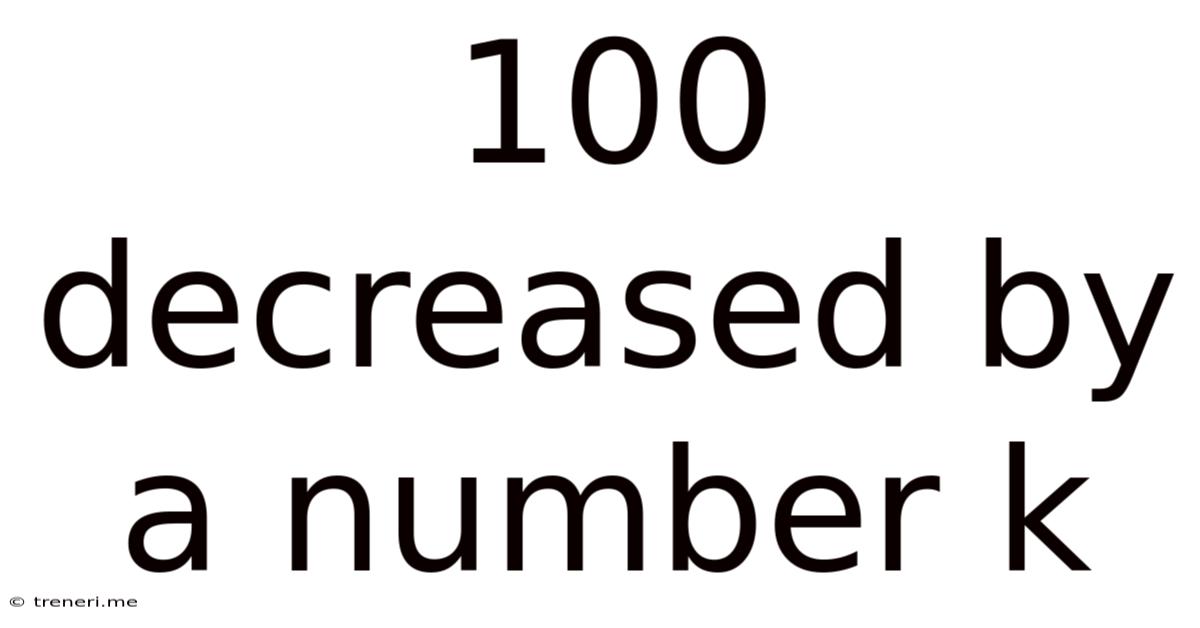
Table of Contents
100 Decreased by a Number k: Exploring Mathematical Concepts and Real-World Applications
The seemingly simple phrase "100 decreased by a number k" opens doors to a vast landscape of mathematical concepts and practical applications. This seemingly basic algebraic expression, represented as 100 - k, provides a foundation for understanding variables, equations, inequalities, and their relevance in various fields. This article will delve deep into this expression, exploring its mathematical implications, practical uses, and how it connects to broader mathematical principles.
Understanding the Expression: 100 - k
At its core, "100 decreased by a number k" translates directly into the algebraic expression 100 - k. Here:
- 100 represents a constant value. It remains unchanged regardless of the value of k.
- k represents a variable. This means its value can change. It's a placeholder for any number – positive, negative, or zero.
- - signifies subtraction. This operation reduces the constant value (100) by the value of the variable (k).
The expression itself is a simple binomial – a polynomial with two terms. Understanding this seemingly straightforward expression is crucial for grasping more complex mathematical concepts.
Exploring Different Values of k
The beauty of this expression lies in its versatility. Let's explore the outcome with different values of k:
- If k = 0: 100 - 0 = 100. The result is unchanged.
- If k = 25: 100 - 25 = 75. The result is 75.
- If k = 100: 100 - 100 = 0. The result is zero.
- If k = -50: 100 - (-50) = 150. Subtracting a negative number is equivalent to adding its positive counterpart. The result is 150.
- If k = 150: 100 - 150 = -50. The result is a negative number.
This demonstrates how the value of the expression (100 - k) is entirely dependent on the value assigned to k. This dependence is a fundamental concept in algebra and forms the basis for solving equations and inequalities.
Applications in Equations and Inequalities
The expression 100 - k forms the backbone of numerous equations and inequalities. Let's explore some examples:
Solving Equations
Consider the equation: 100 - k = 50
To solve for k, we need to isolate k on one side of the equation. We can achieve this by subtracting 50 from both sides:
100 - k - 50 = 50 - 50
This simplifies to:
50 - k = 0
Adding k to both sides and subtracting 0 from both sides gives:
k = 50
Therefore, when 100 is decreased by 50, the result is 50.
Another example: 100 - k = x
This equation highlights the relationship between the expression (100 - k) and another variable, x. To solve for k, we would need a value for x. For example, if x = 20, then:
100 - k = 20
k = 80
Solving Inequalities
Inequalities introduce another layer of complexity. Consider:
100 - k > 70
This inequality states that "100 decreased by k is greater than 70." To solve this, we follow similar steps to solving equations but need to consider the effect of operations on the inequality sign. Subtracting 100 from both sides yields:
-k > -30
Multiplying both sides by -1 (and reversing the inequality sign):
k < 30
This means that k must be less than 30 for the inequality to hold true.
Similarly, consider: 100 - k ≤ 20
Solving this inequality:
-k ≤ -80
k ≥ 80
This means k must be greater than or equal to 80.
Real-World Applications
The seemingly abstract concept of "100 decreased by a number k" finds numerous real-world applications across various fields:
Finance and Budgeting
Imagine you have a budget of $100. The expression 100 - k can represent the remaining amount after spending k dollars. This is vital for personal finance management, tracking expenses, and ensuring you stay within your budget.
Inventory Management
A warehouse has 100 units of a particular product. If k units are sold, then 100 - k represents the remaining inventory. This is crucial for effective inventory control and preventing stockouts or overstocking.
Temperature Changes
If the initial temperature is 100 degrees and it decreases by k degrees, then 100 - k represents the final temperature. This simple expression finds its application in meteorology and climatology for tracking temperature fluctuations.
Measurement and Conversions
In conversion problems, if a length of 100 units is reduced by k units, 100 - k gives the resulting length.
Expanding the Concept: Beyond 100
The principles discussed above extend far beyond the specific number 100. The general form of the expression is a - k, where 'a' is a constant and k is a variable. This generalized expression allows us to analyze a wide range of scenarios involving reduction or decrease. The constant 'a' could represent any quantity—money, weight, distance, time, or any measurable attribute.
The mathematical operations and problem-solving techniques remain the same regardless of the specific value of 'a'. This emphasizes the power of algebra in providing a generalized framework to handle diverse situations.
Connecting to Broader Mathematical Concepts
The simple expression 100 - k provides a springboard to explore more advanced mathematical topics:
- Functions: The expression can be viewed as a function, where k is the input and 100 - k is the output. This leads to exploring function notation, domain, and range.
- Graphing: The expression can be graphed on a coordinate plane, providing a visual representation of the relationship between k and 100 - k. This allows for a better understanding of how changes in k affect the output.
- Calculus: While beyond the scope of this article, the concepts here form the foundation for understanding derivatives and rates of change – crucial elements of calculus.
Conclusion
The seemingly simple expression "100 decreased by a number k" is far more significant than it initially appears. Its exploration unravels fundamental concepts in algebra, equations, inequalities, and their numerous real-world applications. Understanding this expression lays a solid groundwork for tackling more complex mathematical problems and appreciating the power of mathematical modeling in solving real-world challenges across diverse fields. The versatility and applicability of this basic expression highlight the importance of building a strong foundation in elementary mathematics. This foundation provides the tools to interpret, analyze, and solve problems in numerous scenarios, ultimately enhancing critical thinking and problem-solving skills.
Latest Posts
Latest Posts
-
How Many Grams Equal A Half Ounce
May 10, 2025
-
How Many Sides Are On An Octagon
May 10, 2025
-
30 X 46 Rug In Feet
May 10, 2025
-
Find The Length Of The Segment Ab
May 10, 2025
-
What Fraction Is Equivalent To 4 9
May 10, 2025
Related Post
Thank you for visiting our website which covers about 100 Decreased By A Number K . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.