11 Is 50 Of What Number
Treneri
May 07, 2025 · 4 min read
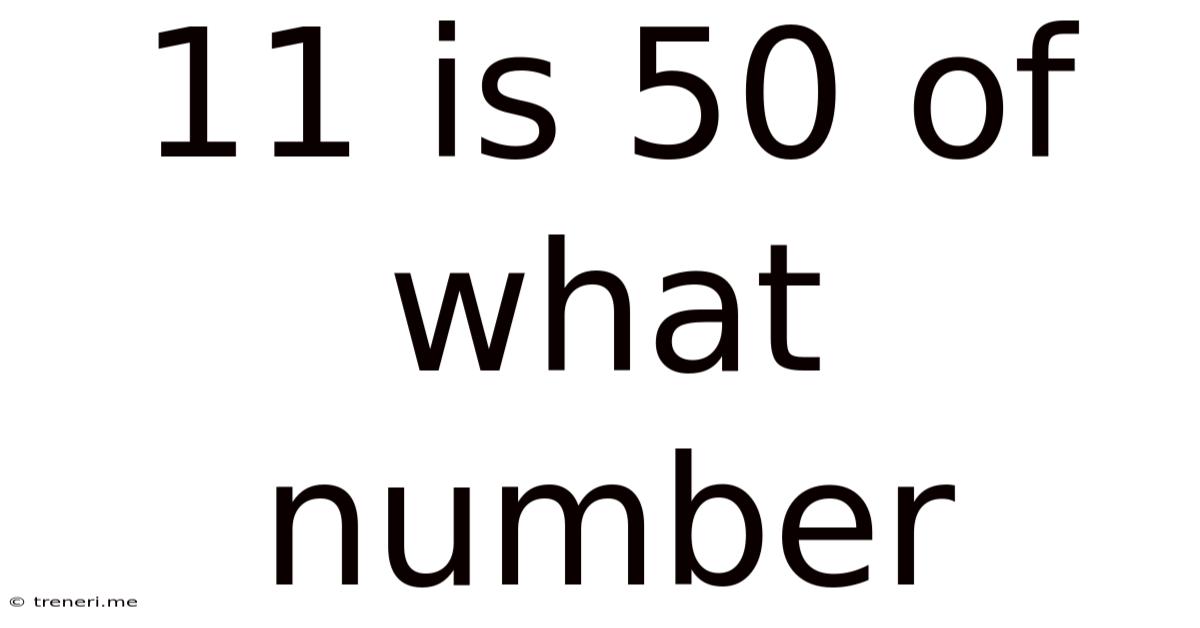
Table of Contents
11 is 50% of What Number? A Deep Dive into Percentage Calculations
Solving the equation "11 is 50% of what number?" might seem straightforward, but it opens the door to understanding fundamental concepts in mathematics, particularly percentages and their applications in various fields. This article will not only provide the solution but also explore the underlying principles, alternative methods, and real-world scenarios where such calculations are crucial. We'll even delve into more complex percentage problems to build your confidence and skills.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." This means 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental relationship is key to solving percentage problems.
Key Percentage Concepts:
- Percentage: The portion of a whole represented as a number out of 100.
- Base: The original number or whole upon which the percentage is calculated. This is the number we're trying to find in our problem.
- Amount: The part of the base represented by the percentage. In our problem, the amount is 11.
Solving "11 is 50% of What Number?"
Let's tackle the core question: 11 is 50% of what number?
We can solve this using several methods:
Method 1: Algebraic Approach
Let's represent the unknown number with the variable 'x'. We can translate the problem into an algebraic equation:
11 = 0.5 * x
To solve for x, we divide both sides of the equation by 0.5:
x = 11 / 0.5
x = 22
Therefore, 11 is 50% of 22.
Method 2: Proportion Method
We can also solve this using proportions. We set up a proportion where one ratio represents the percentage (50/100) and the other represents the given amount (11/x):
50/100 = 11/x
Cross-multiplying gives us:
50x = 1100
Dividing both sides by 50:
x = 22
Again, we find that 11 is 50% of 22.
Method 3: Using the Percentage Formula
The basic percentage formula is:
Amount = (Percentage/100) * Base
In our case:
11 = (50/100) * x
Simplifying and solving for x, we get:
11 = 0.5x
x = 22
This confirms our previous results.
Expanding Your Understanding: More Complex Percentage Problems
Now that we've mastered the basics, let's tackle more complex scenarios to further solidify your understanding of percentage calculations.
Scenario 1: Finding the Percentage Increase or Decrease
Suppose a product's price increased from $20 to $25. What is the percentage increase?
First, calculate the difference: $25 - $20 = $5
Then, divide the difference by the original price and multiply by 100:
($5 / $20) * 100 = 25%
The price increased by 25%.
Scenario 2: Calculating Discounts
A store offers a 30% discount on an item originally priced at $80. What is the sale price?
First, calculate the discount amount: 30% of $80 = (30/100) * $80 = $24
Then, subtract the discount from the original price: $80 - $24 = $56
The sale price is $56.
Scenario 3: Calculating Tax
A restaurant bill is $75, and the sales tax is 6%. What is the total amount including tax?
First, calculate the tax amount: 6% of $75 = (6/100) * $75 = $4.50
Then, add the tax to the original bill: $75 + $4.50 = $79.50
The total amount including tax is $79.50.
Scenario 4: Compound Interest
Imagine you invest $1000 at an annual interest rate of 5%, compounded annually. What will be the balance after two years?
Year 1: $1000 * 0.05 = $50 interest. Balance: $1000 + $50 = $1050
Year 2: $1050 * 0.05 = $52.50 interest. Balance: $1050 + $52.50 = $1102.50
After two years, the balance will be $1102.50.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life and across numerous professions:
- Finance: Calculating interest rates, loan repayments, investment returns, and tax.
- Retail: Determining discounts, sales tax, and profit margins.
- Science: Expressing experimental results, statistical analysis, and error margins.
- Education: Grading systems, test scores, and performance evaluations.
- Everyday Life: Tipping in restaurants, calculating sales tax on purchases, understanding nutritional information on food labels.
Mastering Percentages: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Understand the Concepts: Focus on grasping the underlying principles rather than just memorizing formulas.
- Use Multiple Methods: Try different approaches to solving problems to find the method that best suits you.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Utilize Online Resources: Numerous websites and calculators are available to assist you with percentage calculations.
Conclusion: Beyond the Basics
This article has explored the solution to "11 is 50% of what number?" and expanded upon the fundamental concepts of percentage calculations. By understanding the underlying principles and practicing various problem types, you'll develop the skills to confidently tackle a wide range of percentage-related challenges in both academic and real-world situations. Remember, mastering percentages is a valuable skill that will enhance your problem-solving abilities and contribute to success in various aspects of life.
Latest Posts
Latest Posts
-
Find Polar Coordinates Of The Point That Has Rectangular Coordinates
May 11, 2025
-
Calculate The Weighted Mean Of The Following Data
May 11, 2025
-
What Is 70 Percent Of 15
May 11, 2025
-
Shortest Distance From A Point To A Plane
May 11, 2025
-
1 Pound Of Peanut Butter Equals How Many Cups
May 11, 2025
Related Post
Thank you for visiting our website which covers about 11 Is 50 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.