11 Out Of 30 As A Percentage
Treneri
May 11, 2025 · 5 min read
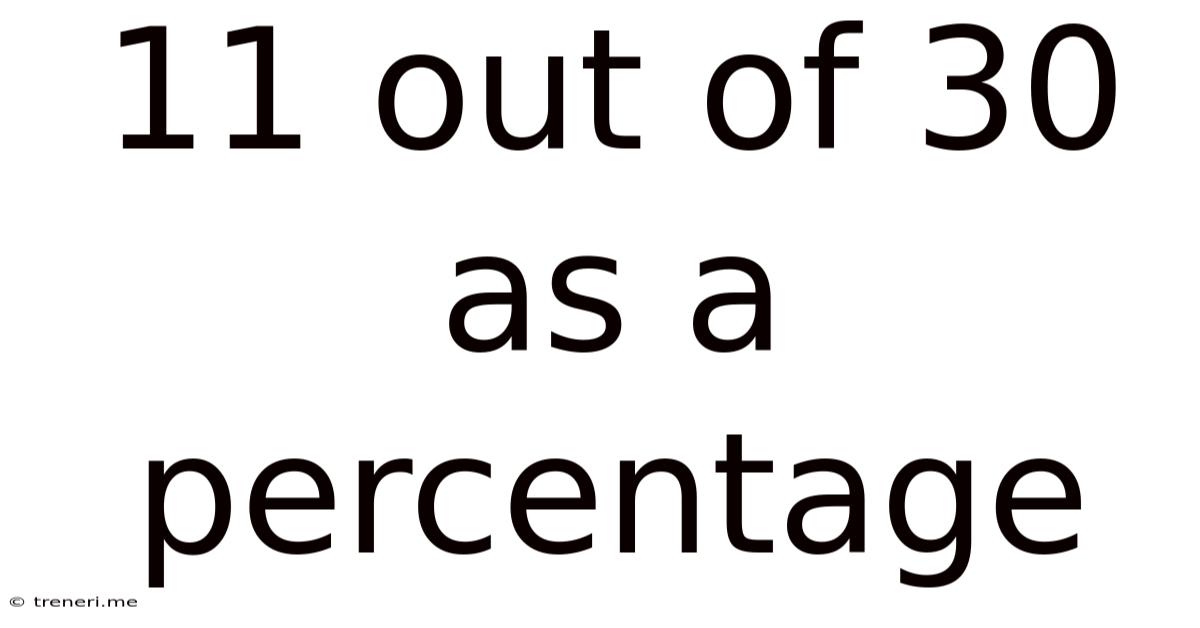
Table of Contents
11 Out of 30 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This comprehensive guide will delve into the calculation of 11 out of 30 as a percentage, explaining the process step-by-step and exploring related concepts to solidify your understanding of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." Therefore, when we say "x%," we mean x out of 100, or x/100. Percentages are a convenient way to represent proportions and make comparisons. They're widely used to express probabilities, discounts, changes, and many other quantitative relationships.
Calculating 11 Out of 30 as a Percentage
To calculate 11 out of 30 as a percentage, we follow these simple steps:
Step 1: Formulate the Fraction
First, express the given information as a fraction. "11 out of 30" translates directly into the fraction 11/30.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (11) by the denominator (30):
11 ÷ 30 = 0.366666...
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.366666... × 100 ≈ 36.67%
Therefore, 11 out of 30 is approximately 36.67%. The recurring decimal is typically rounded to two decimal places for practical purposes.
Different Ways to Calculate Percentages
While the above method is the most straightforward, several alternative approaches can achieve the same result:
Method 1: Using Proportions
We can set up a proportion to solve this problem:
11/30 = x/100
Cross-multiplying gives:
30x = 1100
Solving for x:
x = 1100/30 ≈ 36.67
Therefore, x ≈ 36.67%, confirming our previous calculation.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply input 11 ÷ 30 and then multiply the result by 100 to obtain the percentage.
Method 3: Using Spreadsheet Software
Spreadsheets like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. The formula =(11/30)*100 will directly return the percentage.
Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Academic Performance:
Calculating grades, class averages, and individual progress often involves percentages. For instance, if a student scores 11 out of 30 on a test, their percentage score is 36.67%.
2. Financial Analysis:
Businesses use percentages extensively for profit margins, interest rates, return on investment (ROI), and financial ratios. For example, calculating the percentage change in sales revenue between two periods is a vital aspect of financial analysis.
3. Sales and Discounts:
Retail stores commonly use percentages to advertise discounts and sales. A "30% off" sale means a reduction of 30% of the original price.
4. Statistical Analysis:
Percentages are essential in statistical analysis to represent proportions within datasets and to interpret probabilities. For instance, a survey might reveal that 36.67% of respondents favor a particular product.
5. Scientific Research:
Scientific research often utilizes percentages to represent experimental results, data analysis, and error margins.
Beyond the Basics: Advanced Percentage Concepts
While calculating 11 out of 30 as a percentage is relatively straightforward, understanding more advanced percentage concepts can enhance your analytical skills:
1. Percentage Change:
This calculates the increase or decrease in a value expressed as a percentage. The formula is:
[(New Value - Old Value) / Old Value] x 100
For example, if sales increased from 100 units to 111 units, the percentage increase is:
[(111 - 100) / 100] x 100 = 11%
2. Percentage Points:
Percentage points represent the absolute difference between two percentages. It's crucial not to confuse percentage points with percentage changes. For example, if interest rates rise from 5% to 8%, the increase is 3 percentage points, not 3%.
3. Compound Interest:
This involves calculating interest on both the principal amount and accumulated interest. The formula is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
4. Percentage Points vs. Percentage Change: A Clear Distinction
It is crucial to understand the difference between percentage points and percentage change. A change of 3 percentage points means a direct addition or subtraction of 3% to the original percentage. For example, if inflation rises from 2% to 5%, it increased by 3 percentage points. However, the percentage change is calculated as [(5-2)/2] * 100 = 150%, indicating a 150% increase relative to the initial value. This distinction is important for accurate interpretation and reporting of data.
Conclusion
Calculating 11 out of 30 as a percentage, resulting in approximately 36.67%, is a basic yet essential skill with widespread applications. Understanding the underlying principles of percentage calculations, including the various methods for determining percentages and the advanced concepts, equips you with a valuable tool for navigating numerous quantitative challenges in various fields. By mastering these concepts, you can confidently interpret data, make informed decisions, and effectively communicate quantitative information. Remember to pay close attention to the context and the specific requirements of the problem to ensure accurate interpretation and application of percentages.
Latest Posts
Latest Posts
-
Can You Get A Tan With Uv 4
May 12, 2025
-
How Many Days Are 3000 Hours
May 12, 2025
-
How Many Knuts In A Galleon
May 12, 2025
-
What Is The Correct Length Of A Tie
May 12, 2025
-
Cuantos Dias Faltan Para El 24 De Marzo
May 12, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.