12.5 Is 8 Of What Number
Treneri
May 13, 2025 · 4 min read
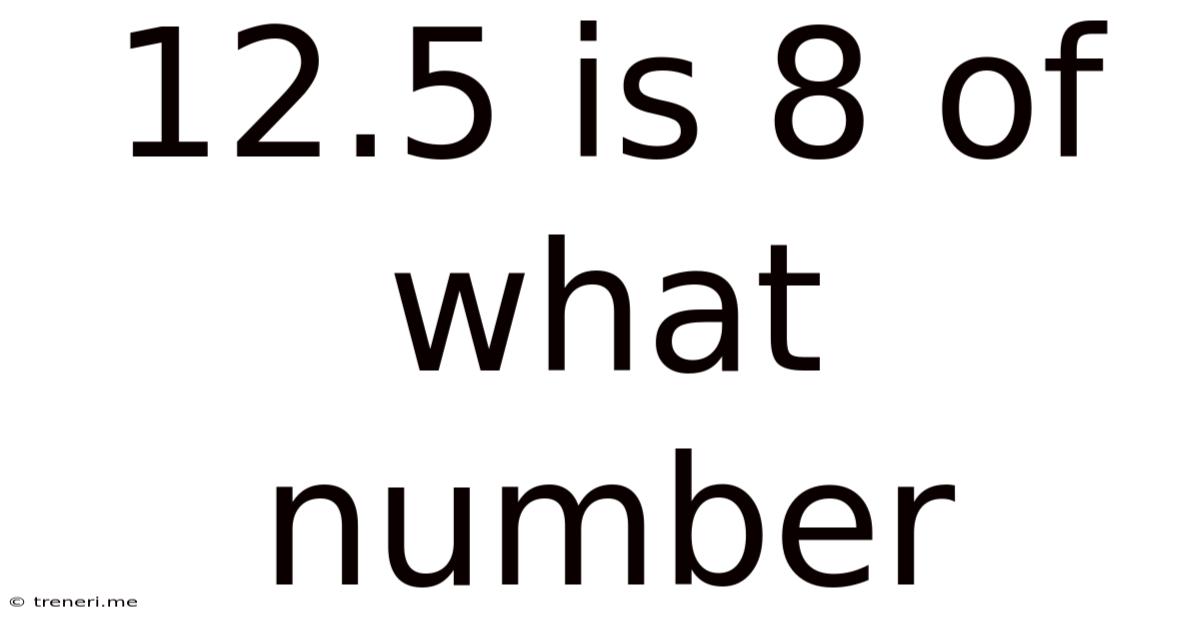
Table of Contents
12.5 is 8% of What Number? A Comprehensive Guide to Percentage Calculations
This article will delve into the problem of finding the original number when you know a percentage of it. Specifically, we'll tackle the question: 12.5 is 8% of what number? We'll explore multiple approaches to solving this, from basic arithmetic to using algebraic equations, ensuring you gain a complete understanding of percentage calculations. This guide is designed to be accessible to everyone, from those just starting to learn percentages to those looking to solidify their understanding.
Understanding the Problem
Before jumping into the solutions, let's clarify what the problem is asking. We're given that 12.5 represents 8% of an unknown number. Our goal is to find this unknown number. This type of problem frequently appears in various contexts, including:
- Financial calculations: Determining the original price before a discount.
- Statistical analysis: Finding the total population based on a sample percentage.
- Everyday life: Calculating the total amount based on a given percentage increase or decrease.
Method 1: Using Proportions
One of the most straightforward ways to solve this problem is using proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion based on the given information:
8% / 100% = 12.5 / x
Where 'x' represents the unknown number we're trying to find.
This proportion can be read as: "8 percent is to 100 percent as 12.5 is to x."
To solve for x, we can cross-multiply:
8% * x = 12.5 * 100%
8x = 1250
x = 1250 / 8
x = 156.25
Therefore, 12.5 is 8% of 156.25.
Method 2: Using the Decimal Equivalent of a Percentage
Percentages can be easily converted to decimals by dividing by 100. In this case, 8% is equivalent to 0.08 (8 / 100 = 0.08). We can then use this decimal to set up an equation:
0.08 * x = 12.5
To solve for x, we divide both sides of the equation by 0.08:
x = 12.5 / 0.08
x = 156.25
Again, we arrive at the solution: 12.5 is 8% of 156.25.
Method 3: Applying the Percentage Formula
The general formula for calculating percentages is:
Percentage = (Part / Whole) * 100%
In our problem, we know the percentage (8%) and the part (12.5). We need to find the whole (x). Rearranging the formula to solve for the whole, we get:
Whole = (Part / Percentage) * 100%
Substituting the known values:
x = (12.5 / 8) * 100
x = 1.5625 * 100
x = 156.25
This method confirms our previous results: 12.5 is 8% of 156.25.
Method 4: Using Algebra
We can represent the problem algebraically. Let 'x' be the unknown number. The problem can be translated into the equation:
0.08x = 12.5
To solve for x, we divide both sides by 0.08:
x = 12.5 / 0.08
x = 156.25
This algebraic approach reinforces the solution: 12.5 is 8% of 156.25.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial for various real-world scenarios. Here are some examples:
-
Sales and discounts: A store offers an 8% discount on an item, and the discount amount is $12.50. Using the methods described above, we can determine the original price of the item was $156.25.
-
Tax calculations: If a sales tax of 8% amounts to $12.50, the pre-tax price of the item was $156.25.
-
Investment returns: An investment yields an 8% return of $12.50. The initial investment amount was $156.25.
-
Statistical surveys: If 8% of respondents in a survey (12.5 people) answered a question in a certain way, the total number of respondents was 156.25. (Note: In real-world surveys, you'll always have whole numbers of people, so this would need rounding.)
Troubleshooting Common Mistakes
When working with percentages, several common mistakes can occur:
-
Incorrect decimal conversion: Remember to divide the percentage by 100 to convert it to a decimal before performing calculations. For example, 8% is 0.08, not 0.8.
-
Mixing up the parts and the whole: Ensure you correctly identify the part (the percentage amount) and the whole (the total amount).
-
Calculation errors: Double-check your arithmetic to avoid errors in division or multiplication.
Advanced Percentage Problems
While this article focuses on a specific problem, the methods discussed can be applied to a wider range of percentage problems, including those involving multiple percentages, percentage increases or decreases, and compound interest. Understanding these fundamental principles will equip you to tackle more complex percentage calculations.
Conclusion
The question "12.5 is 8% of what number?" can be solved using several methods, all yielding the same answer: 156.25. By mastering these methods – proportions, decimal conversion, the percentage formula, and algebraic equations – you'll develop a strong foundation in percentage calculations. This understanding is valuable in various academic and real-world contexts, from finance and statistics to everyday shopping and decision-making. Remember to practice regularly to solidify your skills and confidently tackle even more complex percentage problems.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 24 And 84
May 13, 2025
-
What Is The Gcf Of 70 And 28
May 13, 2025
-
What Size Bbq Grill Do I Need
May 13, 2025
-
3 2 Rounded To The Nearest Tenth
May 13, 2025
-
What Is The Greatest Common Factor Of 72 And 84
May 13, 2025
Related Post
Thank you for visiting our website which covers about 12.5 Is 8 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.