12 Is 40 Percent Of What
Treneri
May 11, 2025 · 5 min read
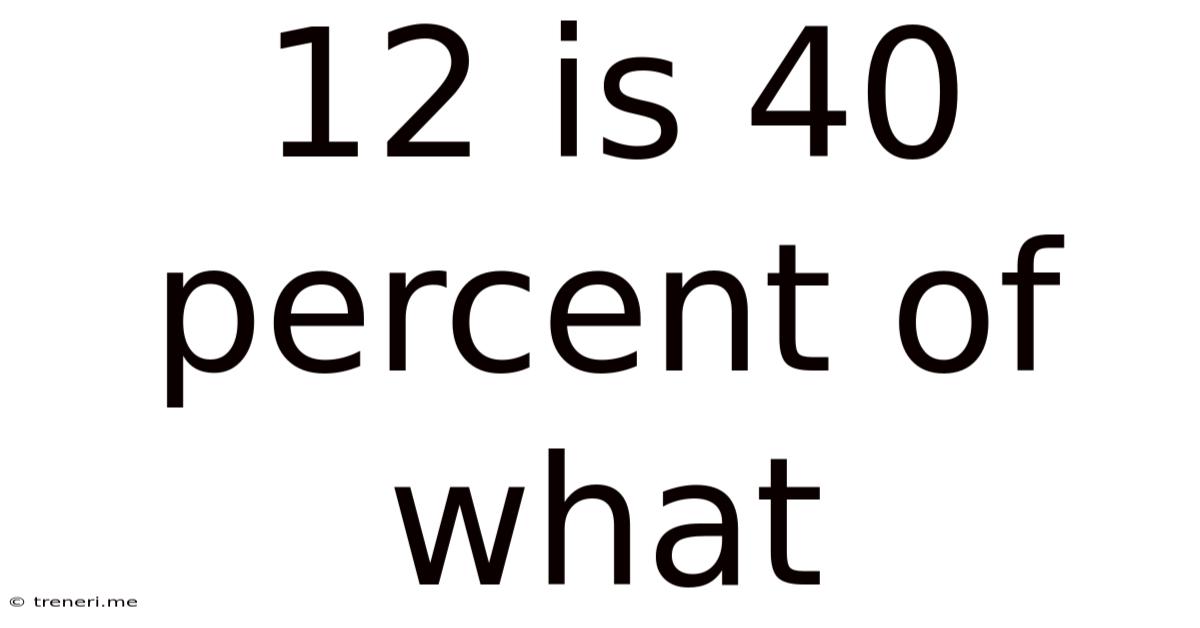
Table of Contents
12 is 40 Percent of What: A Comprehensive Guide to Percentage Calculations
Many everyday situations require understanding percentages. Whether you're calculating discounts, figuring out tax amounts, or determining the size of a population segment, mastering percentage calculations is crucial. This comprehensive guide will delve into the question, "12 is 40 percent of what," explaining the method and providing various applications and practical examples. We'll also explore related percentage problems and how to solve them confidently.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" represents "percent," meaning "out of 100." For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5. Understanding this fundamental concept is vital for solving percentage problems.
Solving "12 is 40 Percent of What"
The core of this problem lies in translating the phrase into a mathematical equation. Let's break it down step-by-step:
- "12 is": This translates to 12 =
- "40 percent": This translates to 0.40 (because 40% = 40/100 = 0.40)
- "of what": This represents the unknown value we need to find. Let's denote this unknown value as 'x'.
Therefore, the equation becomes:
12 = 0.40x
To solve for 'x', we perform the following steps:
-
Divide both sides of the equation by 0.40: This isolates 'x' on one side of the equation.
12 / 0.40 = x
-
Calculate the result:
x = 30
Therefore, 12 is 40 percent of 30.
Different Approaches to Solving Percentage Problems
While the above method is straightforward, several other approaches can be used to solve similar percentage problems. These alternative methods offer flexibility and can be particularly useful depending on the complexity of the problem.
Method 1: Using Proportions
Proportions provide a visual and intuitive way to solve percentage problems. We can set up a proportion as follows:
- Part/Whole = Percentage/100
In our case:
- 12/x = 40/100
To solve for x, cross-multiply:
- 12 * 100 = 40 * x
- 1200 = 40x
- x = 1200 / 40
- x = 30
This method reinforces the relationship between parts and wholes within percentages.
Method 2: Using the Formula (Is/Of = Percent/100)
This formula provides a structured approach for various percentage problems. "Is" represents the part, "Of" represents the whole, and "Percent" is the percentage value.
Plugging in our values:
- 12/x = 40/100
Cross-multiplying and solving for x will yield the same result: x = 30
Method 3: Working with Decimals
This method directly uses decimal equivalents of percentages. We already used this method in our initial solution. Converting 40% to its decimal equivalent (0.40) simplifies the equation:
- 12 = 0.40x
- x = 12 / 0.40
- x = 30
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond theoretical exercises. They are applied extensively in various real-world scenarios, including:
1. Financial Calculations:
- Discounts: Calculating sale prices, determining savings during promotional periods. For example, a 20% discount on a $100 item results in a $20 discount, bringing the price to $80.
- Taxes: Calculating sales tax, income tax, and other taxes. A 6% sales tax on a $50 purchase adds $3 to the final price.
- Interest Rates: Calculating simple interest, compound interest, and loan repayments. Understanding interest rates is critical for managing personal finances effectively.
- Investment Returns: Assessing returns on investments, determining profit or loss on stocks, bonds, or other investments. A 10% return on a $1000 investment yields a $100 profit.
2. Data Analysis and Statistics:
- Population Proportions: Determining the percentage of a population possessing a specific characteristic. For example, if 15% of a city's population is under 18 years old, understanding the total city population allows for calculating the exact number of people under 18.
- Survey Results: Analyzing survey data to understand the distribution of opinions, preferences, or behaviors within a sample population. If 60% of survey respondents prefer a particular product, it offers valuable insights for businesses.
- Market Research: Analyzing market trends, identifying target demographics, and determining market share. Market research frequently uses percentage to show relative market dominance of various companies.
3. Everyday Life:
- Tipping: Calculating appropriate tips in restaurants or other service settings. A 15% tip on a $50 meal adds $7.50.
- Cooking and Baking: Adjusting recipe quantities based on percentages. If a recipe calls for doubling the ingredients, that essentially means increasing each ingredient by 100%.
- Shopping: Comparing prices and discounts, determining the best value for money, understanding unit costs.
Solving More Complex Percentage Problems
While "12 is 40 percent of what" represents a fundamental percentage problem, many situations require solving more complex variations. Here are some examples and methods to solve them:
Example 1: Finding the percentage increase or decrease:
-
Problem: A product's price increased from $50 to $60. What is the percentage increase?
-
Solution:
- Find the difference: $60 - $50 = $10
- Divide the difference by the original price: $10 / $50 = 0.20
- Multiply by 100 to express as a percentage: 0.20 * 100 = 20% Therefore, the price increased by 20%.
Example 2: Finding the original value after a percentage change:
-
Problem: A product is on sale for $70 after a 30% discount. What was the original price?
-
Solution:
- The sale price represents 70% of the original price (100% - 30% = 70%).
- Let 'x' be the original price. Then 0.70x = $70
- Solve for x: x = $70 / 0.70 = $100 Therefore, the original price was $100.
Example 3: Calculating Percentage Change with Multiple Changes:
-
Problem: A stock price rises by 10% and then falls by 10%. Is the final price the same as the original price?
-
Solution: No, this is a common misconception. Percentage changes are not additive. You must calculate sequentially. Let's say the starting price is $100.
- 10% increase: $100 * 1.10 = $110
- 10% decrease from $110: $110 * 0.90 = $99 Therefore the final price is $99, lower than the original price of $100.
Conclusion: Mastering Percentages for Success
Understanding percentage calculations is a fundamental skill with wide-ranging applications in various aspects of life. From everyday transactions to complex financial modeling, mastering percentage problems enables informed decision-making and problem-solving. By learning different methods and practicing regularly, you can confidently tackle percentage calculations and use them to your advantage. Remember the core principle: a percentage is simply a fraction out of 100, and by using this understanding and the methods provided, you can solve even the most challenging percentage problems. Keep practicing, and you'll become proficient in navigating the world of percentages.
Latest Posts
Latest Posts
-
Cuantos Dias Pasaron Desde 1 De Enero Hasta Hoy
May 11, 2025
-
1 Xicara De Farinha Quantas Gramas
May 11, 2025
-
Do You Lose Calories In The Sauna
May 11, 2025
-
Highest Common Factor Of 14 And 49
May 11, 2025
-
Can You Tan In A Uv Of 6
May 11, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 40 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.