12 Out Of 24 As A Percentage
Treneri
May 11, 2025 · 5 min read
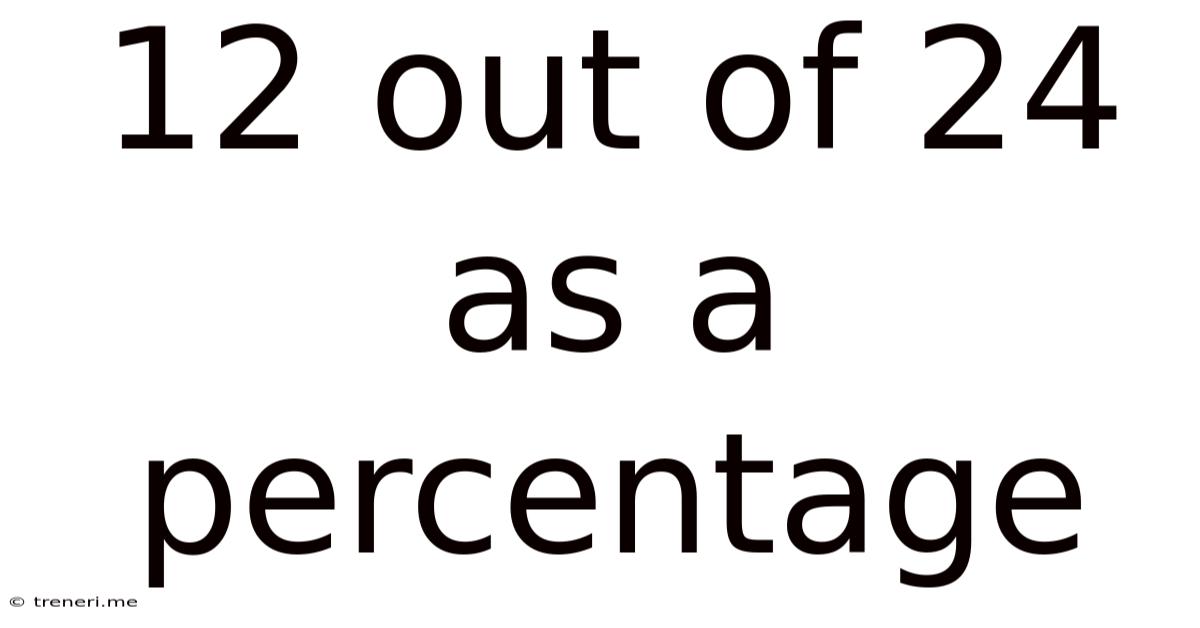
Table of Contents
12 Out of 24 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analysis. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating findings effectively. This comprehensive guide delves into calculating "12 out of 24 as a percentage," explaining the process step-by-step, exploring different methods, and providing practical examples to solidify your understanding. We'll also explore the broader context of percentage calculations and their significance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, or 50/100. Understanding this fundamental concept is key to converting any fraction into a percentage.
Method 1: The Fraction Method
The most straightforward approach to calculating "12 out of 24 as a percentage" is to first express it as a fraction:
12/24
This fraction represents the part (12) over the whole (24). To convert this fraction into a percentage, we need to create an equivalent fraction with a denominator of 100. We can simplify the fraction first:
12/24 = 1/2
Now, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by the same number:
(1 x 50) / (2 x 50) = 50/100
Since 50/100 means 50 out of 100, this fraction is equal to 50%.
Therefore, 12 out of 24 is 50%.
Method 2: The Decimal Method
Another method involves converting the fraction into a decimal first, and then multiplying by 100 to obtain the percentage. Starting with the original fraction:
12/24
Divide the numerator (12) by the denominator (24):
12 ÷ 24 = 0.5
Now, multiply the decimal (0.5) by 100 to express it as a percentage:
0.5 x 100 = 50
Therefore, 12 out of 24 is 50%.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies this calculation. Simply enter 12 ÷ 24 and then press the percentage button (%). The calculator will directly display the result as 50%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just an academic exercise; it's a vital skill for everyday life and professional contexts. Here are a few examples:
-
Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns all rely on percentage calculations. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase requires converting percentages to decimal values for accurate calculations.
-
Statistics: Percentages are fundamental to data analysis and interpretation. Representing data as percentages provides a standardized and easily understandable way to compare different groups or categories. For example, analyzing survey results, election data, or scientific research often involves expressing results as percentages.
-
Science: Percentage calculations are ubiquitous in scientific fields, from chemistry (concentration calculations) to biology (population growth rates) and physics (efficiency calculations). Accurate percentage calculations are essential for interpreting experimental data and drawing meaningful conclusions.
-
Retail: Discounts, sales tax, and markups are all calculated using percentages. Retailers use percentages to manage pricing, analyze sales performance, and assess profitability.
-
Education: Grade calculations, test scores, and performance evaluations often involve percentages, providing a standard measure of student achievement and progress.
-
Everyday Life: Calculating tips at restaurants, determining the percentage of completion of a project, or understanding nutritional information on food labels all involve using percentages.
Beyond 12 out of 24: Mastering Percentage Calculations
While this guide focuses on "12 out of 24 as a percentage," the principles apply broadly to any fraction or ratio. To calculate any percentage, follow these general steps:
-
Express the situation as a fraction: Identify the part and the whole. The part is the numerator, and the whole is the denominator.
-
Simplify the fraction (optional but recommended): Simplifying the fraction makes the subsequent calculations easier.
-
Convert the fraction to a decimal: Divide the numerator by the denominator.
-
Multiply the decimal by 100: This converts the decimal into a percentage.
-
Add the percentage symbol (%): This signifies that the result is a percentage.
Example: Let's calculate what percentage 15 is of 60.
- Fraction: 15/60
- Simplified Fraction: 1/4
- Decimal: 1 ÷ 4 = 0.25
- Percentage: 0.25 x 100 = 25% Therefore, 15 is 25% of 60.
Advanced Percentage Problems: Dealing with Increases and Decreases
Percentage calculations also extend to scenarios involving increases and decreases. For example:
-
Percentage Increase: If a quantity increases from an initial value to a final value, the percentage increase is calculated as: [(Final Value - Initial Value) / Initial Value] x 100%
-
Percentage Decrease: If a quantity decreases from an initial value to a final value, the percentage decrease is calculated as: [(Initial Value - Final Value) / Initial Value] x 100%
Example: Percentage Increase
A company's revenue increased from $100,000 to $120,000. What is the percentage increase?
Percentage Increase = [(120,000 - 100,000) / 100,000] x 100% = 20%
Example: Percentage Decrease
The price of a product decreased from $50 to $40. What is the percentage decrease?
Percentage Decrease = [(50 - 40) / 50] x 100% = 20%
Conclusion: Mastering Percentages for Success
The ability to calculate percentages accurately is a powerful tool across various aspects of life. Understanding the underlying principles, mastering the different methods (fraction, decimal, calculator), and practicing with diverse examples will equip you with a crucial skill for both personal and professional success. Whether you're analyzing financial data, interpreting scientific results, or simply navigating everyday situations, a solid grasp of percentages will enhance your understanding and decision-making capabilities. Remember to always clearly define the "part" and the "whole" when setting up your calculations to avoid errors. With consistent practice, you'll become proficient in handling percentage calculations with confidence.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 15 And 24
May 12, 2025
-
What Is A Factor Of 46
May 12, 2025
-
How Many Fractions Are Equivalent To 4 5
May 12, 2025
-
500 Sq Ft In Length And Width
May 12, 2025
-
How Long Is 127 Hours In Days
May 12, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.