12 Times Square Root Of 2
Treneri
May 13, 2025 · 5 min read
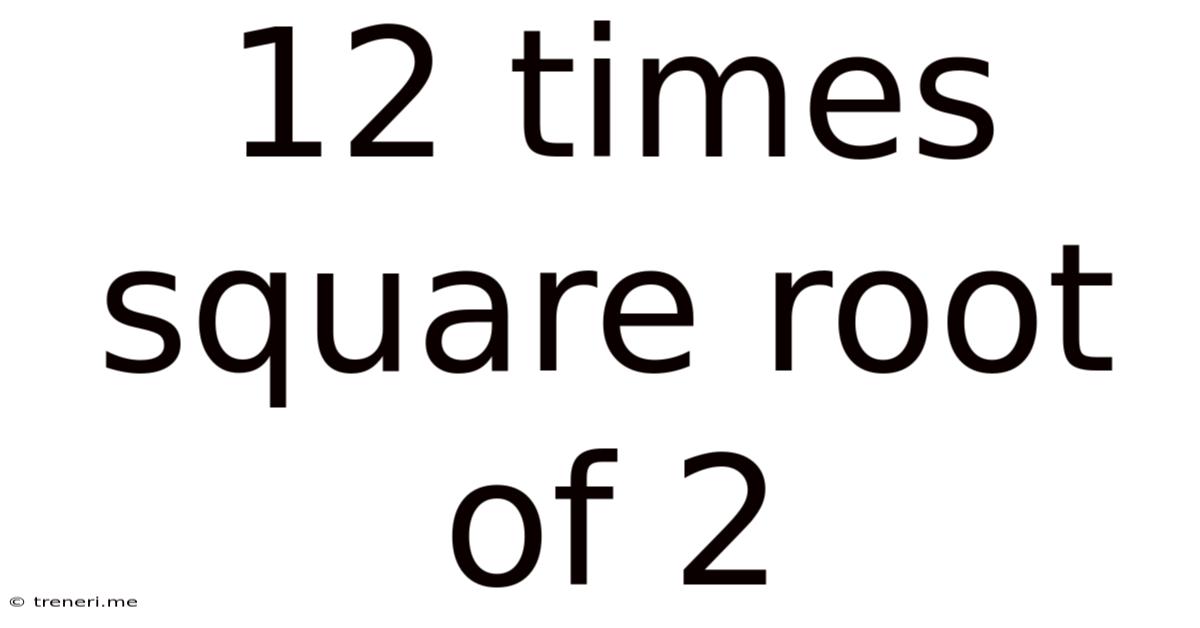
Table of Contents
12 Times the Square Root of 2: Unveiling the Mystery Behind This Mathematical Constant
The seemingly simple expression "12 times the square root of 2" (12√2) hides a surprising depth of mathematical significance and practical applications. While it might not appear as immediately recognizable as π (pi) or e (Euler's number), this constant plays a crucial role in various fields, from geometry and physics to computer graphics and engineering. This article delves into the intricacies of 12√2, exploring its origins, properties, and widespread uses.
Understanding the Basics: Square Roots and Rational Numbers
Before diving into the specifics of 12√2, let's refresh our understanding of square roots and rational numbers. A square root of a number x is a value that, when multiplied by itself, equals x. For instance, the square root of 9 (√9) is 3 because 3 * 3 = 9. The square root of 2 (√2) is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating (approximately 1.41421356...).
This irrationality is key to understanding the nature of 12√2. Multiplying an irrational number (√2) by a rational number (12) doesn't change its fundamental nature; 12√2 remains an irrational number. This seemingly simple multiplication opens doors to a complex world of mathematical possibilities.
The Geometric Significance of 12√2
The number 12√2 frequently appears in geometric calculations, particularly when dealing with diagonals of squares and rectangles. Consider a square with sides of length 12 units. According to the Pythagorean theorem (a² + b² = c²), the length of its diagonal is √(12² + 12²) = √288 = 12√2. This relationship is fundamental in various applications:
Applications in Construction and Design
-
Building structures: The diagonal measurement of 12√2 is crucial in ensuring the precise construction of buildings, bridges, and other structures. Accurate diagonal measurements are essential for maintaining structural integrity and stability. Understanding this constant helps in laying out foundations, ensuring perfect square corners, and checking the accuracy of construction work.
-
Architectural design: In architectural design, understanding 12√2 allows architects to optimize space utilization and create aesthetically pleasing designs. Precise diagonal measurements ensure the proper alignment of walls, doors, and windows, contributing to the overall visual appeal of a building.
-
Engineering drawings: The constant 12√2 appears in numerous engineering drawings, enabling engineers to calculate precise dimensions and ensure proper scaling for projects. Accurate calculations using this constant are vital in the design and manufacturing of various mechanical components and structures.
Applications in Computer Graphics and Game Development
-
Game development: 12√2 and similar calculations are vital in game development, particularly in physics engines. Accurately calculating distances and angles using irrational numbers ensures realistic movement and collision detection within a game environment.
-
Computer graphics: In computer graphics, 12√2 is used to calculate precise positions and orientations of objects within a 2D or 3D space. This precision is particularly crucial in creating realistic and visually appealing graphics.
12√2 in Physics and Other Scientific Fields
Beyond geometry, 12√2 finds its way into various scientific fields, often arising from calculations related to vectors and forces.
Vector Calculations
In physics, vectors are used to represent quantities having both magnitude and direction. The calculation of resultant vectors often involves the square root of 2, leading to expressions like 12√2. For example, if two forces of equal magnitude act at a right angle to each other, the magnitude of the resultant force will involve √2. Multiplying this by a scalar (like 12) scales the resultant force accordingly.
Other Scientific Applications
-
Signal Processing: The number 12√2 and related constants might emerge in signal processing, especially when dealing with phase differences and vector representations of signals.
-
Electromagnetism: Calculations involving electric and magnetic fields can sometimes yield results involving this constant, especially in scenarios with orthogonal components.
Approximations and Practical Considerations
While 12√2 is an irrational number, in practical applications we often need to use an approximation. The degree of accuracy required dictates the number of decimal places used. For many applications, rounding to a few decimal places (e.g., 16.97) provides sufficient accuracy. However, for high-precision applications, more decimal places might be needed. Using calculators or programming languages allows for precise calculations with this constant, avoiding rounding errors.
Beyond the Basics: Exploring Related Concepts
The exploration of 12√2 leads to a deeper understanding of related mathematical concepts:
-
Irrational numbers: The constant highlights the importance of irrational numbers in various fields and the methods for handling them in calculations.
-
Pythagorean theorem: The geometric applications of 12√2 directly relate to the fundamental Pythagorean theorem, emphasizing its significance in both theoretical and practical mathematics.
-
Vector algebra: The application of 12√2 in physics reinforces the power of vector algebra in representing and manipulating physical quantities.
Conclusion: The Ubiquity of 12√2
This exploration reveals that the seemingly simple constant 12√2 has a significant role in numerous fields. Its presence in geometry, physics, computer graphics, and engineering underscores its importance in both theoretical and practical applications. While its irrational nature might seem daunting, its practical applications are readily manageable with the use of modern calculators and computational tools. Understanding this constant and its significance helps us appreciate the profound interconnectedness of mathematics and its applications in the real world. The next time you encounter 12√2, remember its rich history and far-reaching implications across various disciplines. It's a small number with a big impact.
Latest Posts
Latest Posts
-
Round 999 82798406 To 3 Decimal Places
May 14, 2025
-
How Many Pounds Is 56 L
May 14, 2025
-
What Is 25 30 As A Grade
May 14, 2025
-
149 Rounded To The Nearest Hundred
May 14, 2025
-
200 Grams Cream Cheese To Cups
May 14, 2025
Related Post
Thank you for visiting our website which covers about 12 Times Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.