125 Of E Is 30. What Is E
Treneri
May 09, 2025 · 4 min read
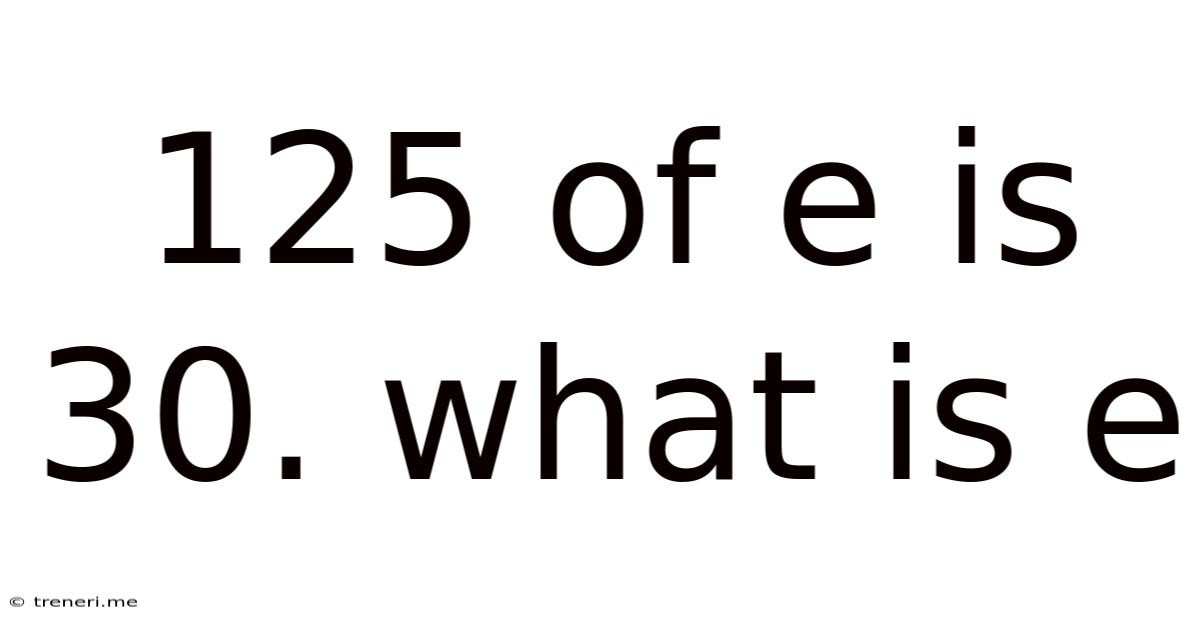
Table of Contents
125% of e is 30. What is e? A Comprehensive Guide to Solving Percentage Problems
This seemingly simple problem, "125% of e is 30. What is e?", opens a door to understanding fundamental concepts in mathematics, specifically percentages and algebraic equations. While the solution might appear straightforward, delving deeper reveals valuable insights applicable to various real-world scenarios, from calculating discounts and interest to analyzing financial data and understanding statistical probabilities. This comprehensive guide will not only provide the solution but will equip you with the knowledge and skills to confidently tackle similar percentage problems.
Understanding Percentages: The Foundation
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, which simplifies to ½ or 0.5.
Converting Percentages to Decimals and Fractions
To solve percentage problems effectively, it's crucial to be able to convert percentages to their decimal and fractional equivalents. To convert a percentage to a decimal, simply divide the percentage by 100. For example:
- 25% = 25/100 = 0.25
- 150% = 150/100 = 1.5
- 0.5% = 0.5/100 = 0.005
To convert a percentage to a fraction, write the percentage as the numerator and 100 as the denominator. Then, simplify the fraction if possible. For example:
- 75% = 75/100 = ¾
- 10% = 10/100 = 1/10
- 33.33% ≈ ⅓ (approximately)
Solving the Problem: 125% of e is 30
Now, let's tackle the problem: "125% of e is 30. What is e?" This statement can be translated into an algebraic equation:
1.25 * e = 30
Here's how we solve it step-by-step:
Step 1: Convert the Percentage to a Decimal
We've already established that 125% is equivalent to 1.25. Substituting this into our equation gives us:
1.25e = 30
Step 2: Isolate the Variable (e)
To find the value of 'e', we need to isolate it on one side of the equation. This is done by dividing both sides of the equation by 1.25:
e = 30 / 1.25
Step 3: Perform the Calculation
Dividing 30 by 1.25 gives us:
e = 24
Therefore, the value of 'e' is 24.
Verifying the Solution
To ensure our solution is correct, let's plug the value of 'e' back into the original equation:
1.25 * 24 = 30
This equation holds true, confirming that our solution, e = 24, is accurate.
Expanding the Understanding: Real-World Applications
The ability to solve percentage problems is invaluable in a wide range of real-world applications. Here are a few examples:
1. Calculating Discounts and Sales Tax
Imagine a shirt is priced at $40, and it's on sale with a 20% discount. To find the sale price, we can use the same principles:
- Discount amount: 20% of $40 = 0.20 * $40 = $8
- Sale price: $40 - $8 = $32
Similarly, calculating sales tax involves finding a percentage of the original price and adding it to the original price.
2. Financial Calculations: Interest and Investments
Understanding percentages is essential for managing personal finances. Calculating simple interest involves finding a percentage of the principal amount. For example, if you invest $1000 at a 5% annual interest rate, the interest earned after one year is:
- Interest earned: 5% of $1000 = 0.05 * $1000 = $50
More complex financial calculations, such as compound interest and loan amortization, also heavily rely on percentage calculations.
3. Data Analysis and Statistics
Percentages are frequently used to represent proportions and probabilities in data analysis and statistics. For instance, expressing survey results, analyzing market share, or determining the likelihood of events all utilize percentages.
4. Everyday Scenarios: Tips, Gratuities, and More
Calculating tips in restaurants, determining the percentage increase or decrease in prices, and understanding commission rates all involve applying percentage concepts.
Advanced Percentage Problems and Techniques
While the initial problem was relatively straightforward, many percentage problems can be more complex. Here are some advanced techniques:
1. Finding the Original Value After a Percentage Change
Suppose the price of an item increased by 15% to $57.50. To find the original price, let's denote the original price as 'x':
x + 0.15x = $57.50
Combining like terms:
1.15x = $57.50
Solving for x:
x = $57.50 / 1.15 = $50
Therefore, the original price was $50.
2. Successive Percentage Changes
When dealing with multiple percentage changes applied sequentially, it's important to note that the percentages don't simply add up. For example, a 20% increase followed by a 20% decrease does not result in the original value. Each percentage change is applied to the new value after the previous change.
3. Using Proportions to Solve Percentage Problems
Percentage problems can also be solved using proportions. For example, if 30% of a number is 60, we can set up a proportion:
30/100 = 60/x
Cross-multiplying and solving for x gives the total number.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill with far-reaching applications in various fields. The seemingly simple problem, "125% of e is 30," serves as a gateway to comprehending these crucial concepts. By mastering these techniques, you’ll be equipped to tackle a wide array of percentage problems with confidence and solve real-world challenges effectively. Remember that practice is key – the more problems you solve, the stronger your understanding will become. So, grab a pen, paper, and some practice problems and start honing your percentage prowess!
Latest Posts
Latest Posts
-
How To Find Molarity From Absorbance
May 11, 2025
-
Cuantos Dias Faltan Para El 19 De Noviembre
May 11, 2025
-
Arranging Numbers From Least To Greatest
May 11, 2025
-
How Long Ago Was 1000 Bc
May 11, 2025
-
90 Days From May 4 2024
May 11, 2025
Related Post
Thank you for visiting our website which covers about 125 Of E Is 30. What Is E . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.