15 Is 25 Percent Of What Number
Treneri
May 09, 2025 · 4 min read
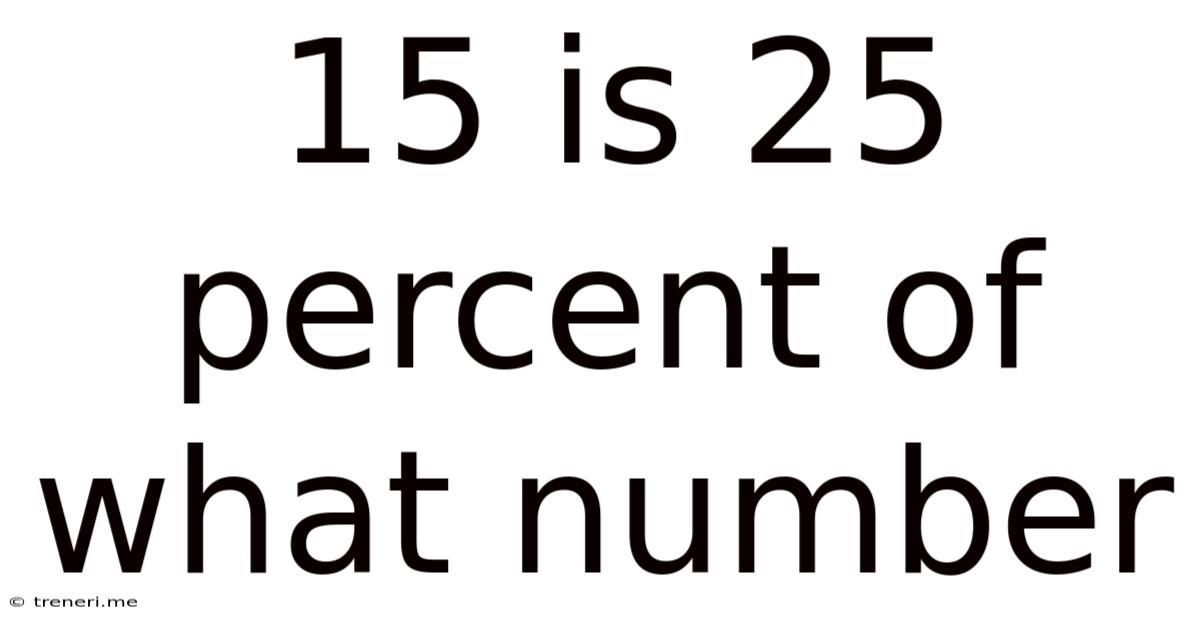
Table of Contents
15 is 25 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article delves into the question, "15 is 25 percent of what number?" We'll not only solve this specific problem but also explore the underlying principles of percentage calculations, offering various methods to tackle similar problems and equipping you with the knowledge to confidently handle percentage-related questions in the future.
Understanding Percentages: The Basics
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Method 1: Using the Proportion Method
This is perhaps the most intuitive method for solving percentage problems. We set up a proportion, equating two ratios:
- Ratio 1: Represents the given percentage (25%) as a fraction (25/100).
- Ratio 2: Represents the unknown number (let's call it 'x') as a ratio to the given part (15).
This sets up the proportion:
25/100 = 15/x
To solve for 'x', we cross-multiply:
25 * x = 15 * 100
25x = 1500
x = 1500 / 25
x = 60
Therefore, 15 is 25% of 60.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then setting up an equation. We know that 25% is equal to 0.25 (25/100). We can then express the problem as an equation:
0.25 * x = 15
To solve for 'x', we divide both sides of the equation by 0.25:
x = 15 / 0.25
x = 60
Again, we find that 15 is 25% of 60.
Method 3: Using the Formula Method
A more formal approach uses the following formula:
Part / Whole = Percentage / 100
In our problem:
- Part = 15
- Percentage = 25
- Whole = x (the unknown number)
Substituting these values into the formula:
15 / x = 25 / 100
Cross-multiplying:
15 * 100 = 25 * x
1500 = 25x
x = 1500 / 25
x = 60
This method confirms, once again, that 15 is 25% of 60.
Real-World Applications: Why This Matters
Understanding percentage calculations isn't just about solving mathematical problems; it's a crucial skill for navigating everyday situations. Here are some real-world applications:
1. Sales and Discounts:
Imagine a store offering a 25% discount on an item. If the discount amount is $15, you can use this method to calculate the original price of the item.
2. Taxes and Interest:
Calculating taxes on purchases or interest accrued on loans often involves percentage calculations.
3. Financial Analysis:
Investors and financial analysts frequently use percentages to analyze financial statements, growth rates, and returns on investment.
4. Statistical Data Interpretation:
Percentages are essential for understanding and interpreting statistical data, such as survey results, population demographics, and scientific research findings. Understanding percentage changes allows for the comparison of data across various time periods.
5. Everyday Budgeting:
Budgeting involves allocating a percentage of your income to different expenses such as housing, food, and transportation.
Expanding Your Percentage Calculation Skills
Mastering percentage calculations opens doors to solving a wide range of problems. Here are some tips for expanding your skills:
1. Practice Regularly:
The more you practice, the more comfortable you'll become with different percentage calculation methods.
2. Work Through Diverse Problems:
Try solving problems that involve different percentages, parts, and wholes to broaden your understanding and build your problem-solving flexibility. This will help you develop an intuition for how percentages work in different contexts.
3. Utilize Online Resources and Tools:
Numerous online resources, calculators, and tutorials are available to help you practice and improve your percentage calculation skills. These tools can provide instant feedback and help you identify areas where you might need extra practice.
4. Learn to Estimate:
Developing an ability to quickly estimate percentages can be very helpful in everyday situations. For example, knowing that 25% is one-quarter can help you quickly approximate discounts or proportions.
Beyond the Basics: Advanced Percentage Problems
While the problem "15 is 25% of what number" is relatively straightforward, percentage problems can become more complex. Here are some examples of more advanced problems:
- Percentage Increase/Decrease: Calculating the percentage change between two numbers.
- Compound Interest: Understanding how interest accumulates over time.
- Percentage of a Percentage: Calculating a percentage of a percentage (e.g., finding 10% of 25% of a number).
Solving these more advanced problems often requires a combination of the techniques outlined above and a strong grasp of algebraic principles.
Conclusion: Mastering the Power of Percentages
Understanding and mastering percentage calculations is a valuable life skill. It empowers you to solve everyday problems, interpret data effectively, and make informed decisions in various aspects of your life. By understanding the fundamental methods and practicing regularly, you can build confidence and proficiency in handling percentages, whether it's calculating discounts, analyzing financial statements, or simply understanding statistical information. The simple problem of "15 is 25 percent of what number" serves as a gateway to unlocking a wider world of numerical understanding and practical application. Remember to consistently practice and explore diverse problem sets to solidify your understanding and enhance your problem-solving capabilities.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 3 And 27
May 10, 2025
-
What Is The Greatest Common Factor Of 56 And 32
May 10, 2025
-
Which Quantity Of Heat Is Equal To 200 Joules
May 10, 2025
-
What Day Will It Be 120 Days From Now
May 10, 2025
-
5 Liters Of Fat Is How Many Pounds
May 10, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 25 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.