15 Is 6 Percent Of What Number
Treneri
May 13, 2025 · 4 min read
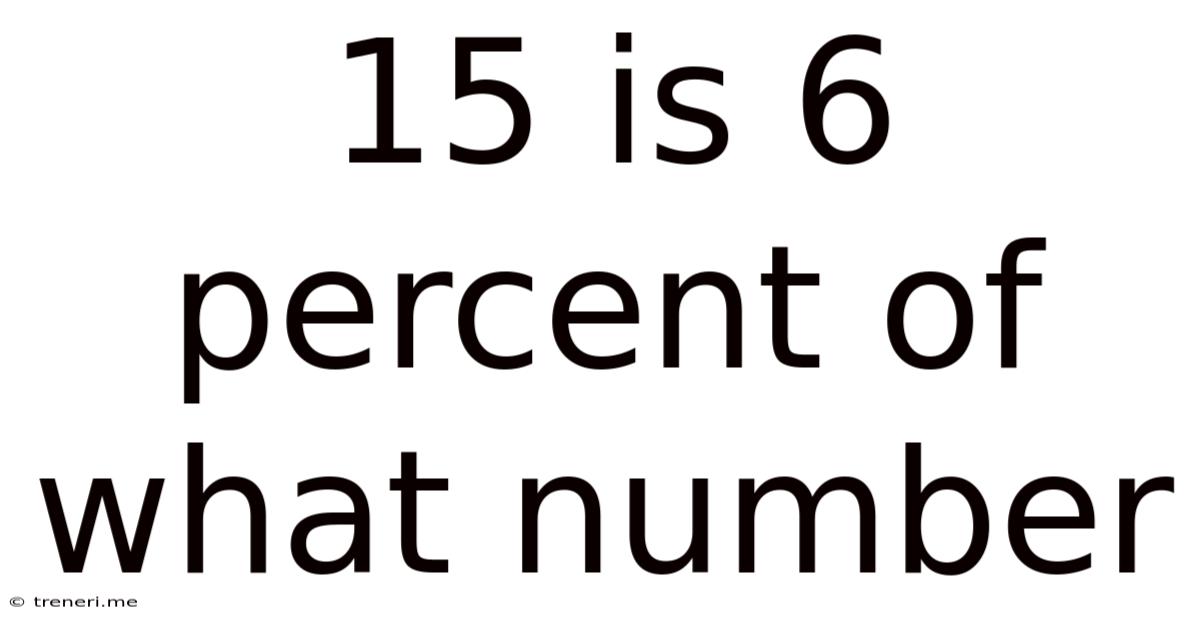
Table of Contents
15 is 6 Percent of What Number: A Comprehensive Guide to Percentage Calculations
This article delves into the solution of the mathematical problem: "15 is 6 percent of what number?" We'll not only provide the answer but also explore the underlying concepts of percentages, demonstrating various methods for solving similar problems. This guide is designed for students, professionals, and anyone looking to improve their understanding of percentage calculations. We'll cover the fundamental principles, offer different approaches to solving the problem, and provide practical examples to solidify your understanding.
Understanding Percentages
Before tackling the main problem, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Concepts:
- Percentage: The portion of a whole, expressed as a number out of 100.
- Whole: The total amount or the base value.
- Part: The portion of the whole represented by the percentage.
Solving "15 is 6 Percent of What Number?"
There are several ways to solve this problem. We'll explore three common methods:
Method 1: Using the Percentage Formula
The most straightforward method involves using the basic percentage formula:
Part = (Percentage/100) * Whole
In our problem:
- Part = 15
- Percentage = 6
- Whole = x (the unknown number)
Substituting these values into the formula, we get:
15 = (6/100) * x
To solve for x, we follow these steps:
- Multiply both sides by 100: 1500 = 6x
- Divide both sides by 6: x = 1500 / 6
- Calculate the result: x = 250
Therefore, 15 is 6 percent of 250.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion:
6/100 = 15/x
This proportion states that 6 is to 100 as 15 is to x. To solve this proportion, we cross-multiply:
6x = 1500
Then, divide both sides by 6:
x = 250
Again, we find that 15 is 6 percent of 250.
Method 3: Using Decimal Equivalents
Percentages can be easily converted into decimals by dividing by 100. In this case, 6% is equal to 0.06. We can rewrite the problem as:
15 = 0.06 * x
Solving for x:
x = 15 / 0.06
x = 250
This method confirms that 15 is 6 percent of 250.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For instance, if a bank offers a 6% interest rate on a savings account, and you earn $15 in interest, you can use this method to determine the principal amount in your savings account.
-
Retail: Discount calculations are frequently encountered in retail settings. If a store offers a 6% discount on an item and the discount amount is $15, you can use the same method to find the original price of the item.
-
Science: Percentages are used extensively in scientific research to represent data and express relationships between variables. For example, if 15 out of 100 participants in a study show a specific characteristic, the percentage of participants exhibiting that characteristic is 15%, allowing for easy comparison and analysis.
-
Statistics: Percentages are essential tools for summarizing and interpreting data in statistics. For instance, determining the percentage of respondents who answered "yes" to a specific survey question is a common application.
Extending Your Understanding: Solving for Different Variables
While we've focused on solving for the "whole," the percentage formula can be rearranged to solve for other variables:
-
Finding the Percentage: If you know the part and the whole, you can solve for the percentage:
Percentage = (Part / Whole) * 100
-
Finding the Part: If you know the percentage and the whole, you can solve for the part using the formula we used earlier:
Part = (Percentage/100) * Whole
Tips for Accurate Percentage Calculations
-
Double-check your work: Always verify your calculations to minimize errors.
-
Use a calculator: For complex calculations, a calculator can improve accuracy and efficiency.
-
Understand the context: Pay close attention to the problem's wording to ensure you're solving for the correct variable.
-
Practice regularly: Consistent practice is key to mastering percentage calculations.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a fundamental skill with broad applications across various fields. By mastering the different methods presented in this article, you'll be well-equipped to tackle a wide range of percentage problems with confidence. Remember to practice regularly and apply these techniques to real-world situations to solidify your understanding and improve your problem-solving abilities. The ability to confidently calculate percentages is a valuable asset in both academic and professional settings, allowing for more accurate analysis and informed decision-making. From financial planning to scientific research, the applications are vast and impactful. So, continue practicing, and watch your proficiency in percentage calculations grow!
Latest Posts
Latest Posts
-
How Far Along Is My Cat Pregnant
May 14, 2025
-
How Many Weeks Is 97 Days
May 14, 2025
-
Cuantos Bloques Entran En Un Metro Cuadrado
May 14, 2025
-
Formula Para Convertir Fahrenheit A Centigrados
May 14, 2025
-
How Much Is 4 6 Quarts
May 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 6 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.