15 Is 70 Percent Of What Number
Treneri
May 14, 2025 · 5 min read
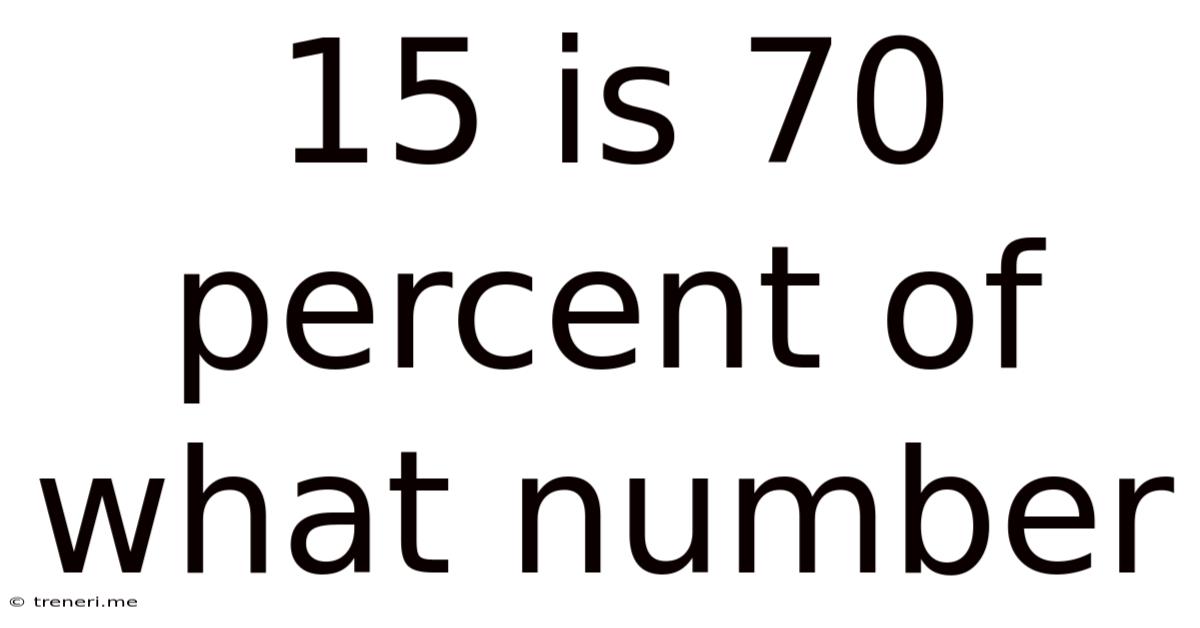
Table of Contents
15 is 70 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Finding a whole number when you know a percentage and its corresponding part is a fundamental mathematical concept with wide-ranging applications. This comprehensive guide will delve into the solution for the problem "15 is 70 percent of what number?", exploring various methods, explaining the underlying principles, and offering practical examples to solidify your understanding. We'll also touch upon the importance of mastering percentage calculations in different fields.
Understanding Percentages and Their Applications
Percentages are a way of expressing a number as a fraction of 100. They are ubiquitous in daily life, from calculating discounts and taxes to understanding statistical data and financial reports. The ability to quickly and accurately calculate percentages is crucial for informed decision-making in various aspects of life, both personal and professional.
Real-World Examples of Percentage Calculations
- Finance: Calculating interest rates, loan repayments, investment returns, and tax deductions all rely heavily on percentage calculations.
- Retail: Determining sale prices, markups, and profit margins requires a firm grasp of percentages.
- Statistics: Analyzing data, interpreting survey results, and understanding population demographics involve working with percentages extensively.
- Science: Many scientific calculations involve expressing results as percentages, such as the percentage of a substance in a solution or the percentage change in a measured quantity.
Methods to Solve "15 is 70 Percent of What Number?"
There are several approaches to finding the answer to this question. Let's explore the most common and effective methods:
Method 1: Using the Proportion Method
This method relies on setting up a proportion, which is an equation stating that two ratios are equal. We can represent the problem as:
15 / x = 70 / 100
Where:
- 15 represents the part.
- x represents the whole number we want to find.
- 70 represents the percentage.
- 100 represents the total percentage (100%).
To solve for x, we can cross-multiply:
15 * 100 = 70 * x
1500 = 70x
Now, divide both sides by 70:
x = 1500 / 70
x ≈ 21.43
Therefore, 15 is approximately 70% of 21.43.
Method 2: Using the Decimal Method
This approach involves converting the percentage to a decimal and then setting up an equation. We know that 70% is equivalent to 0.70 (or 0.7). We can express the problem as:
0.7 * x = 15
To solve for x, divide both sides by 0.7:
x = 15 / 0.7
x ≈ 21.43
Again, we arrive at the same answer: 15 is approximately 70% of 21.43.
Method 3: Using the Formula
A more direct formula can be derived from the proportion method:
Whole Number = (Part / Percentage) * 100
Plugging in our values:
Whole Number = (15 / 70) * 100
Whole Number ≈ 21.43
This formula provides a concise way to calculate the whole number when given a part and its percentage.
Understanding the Significance of Decimal Answers
It's important to note that in many real-world scenarios, the answer might not be a whole number. Rounding to a suitable number of decimal places is often necessary. For example, if we're dealing with money, rounding to two decimal places (cents) is typically sufficient. However, in other contexts, such as scientific calculations, a higher level of precision might be required. Always consider the context of the problem when deciding how to round your answer.
Practical Applications and Advanced Scenarios
The ability to solve percentage problems like "15 is 70 percent of what number?" extends far beyond simple arithmetic exercises. Let's examine some advanced applications:
Scenario 1: Sales and Discounts
A store offers a 30% discount on an item, and the discounted price is $15. What was the original price?
This problem can be solved using the same principles:
Let x be the original price. The discounted price is 70% (100% - 30%) of the original price.
0.7x = 15
x = 15 / 0.7
x ≈ $21.43
The original price was approximately $21.43.
Scenario 2: Investment Returns
An investment grows by 15%, and the profit is $1500. What was the initial investment amount?
The profit represents 15% of the initial investment.
Let x be the initial investment.
0.15x = 1500
x = 1500 / 0.15
x = $10,000
The initial investment amount was $10,000.
Scenario 3: Statistical Analysis
In a survey, 70% of respondents prefer a particular product. If 15 people prefer the product, how many people were surveyed in total?
This directly mirrors our original problem:
Let x be the total number of respondents.
0.7x = 15
x = 15 / 0.7
x ≈ 21.43
Since we can't have a fraction of a person, we round to the nearest whole number. Approximately 21 people were surveyed. (Note that rounding might lead to slight discrepancies; the exact number might be slightly different depending on the rounding method used).
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: Consistent practice is key to mastering percentage calculations. Start with simple problems and gradually work your way up to more complex scenarios.
- Use different methods: Try solving problems using multiple methods to gain a deeper understanding of the underlying principles.
- Utilize online resources: Numerous online calculators and tutorials are available to help you learn and practice percentage calculations.
- Break down complex problems: If faced with a challenging problem, break it down into smaller, more manageable steps.
- Check your answers: Always double-check your answers to ensure accuracy.
Conclusion
The ability to solve percentage problems, such as determining "what number 15 is 70 percent of," is a valuable skill applicable across numerous disciplines. By understanding the different methods and practicing regularly, you can build confidence and competence in tackling percentage calculations effectively. Remember to always consider the context of the problem and round your answers appropriately. This detailed guide equips you with the knowledge and tools to confidently tackle any percentage problem you encounter.
Latest Posts
Latest Posts
-
How Many Calories Do I Burn Pumping
May 14, 2025
-
10 Ml Is The Same As
May 14, 2025
-
How Many Cups In 96 Oz
May 14, 2025
-
What Grade Is A 12 Out Of 18
May 14, 2025
-
What Is An 80 Out Of 100
May 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 70 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.