15 Is 80 Percent Of What Number
Treneri
May 14, 2025 · 4 min read
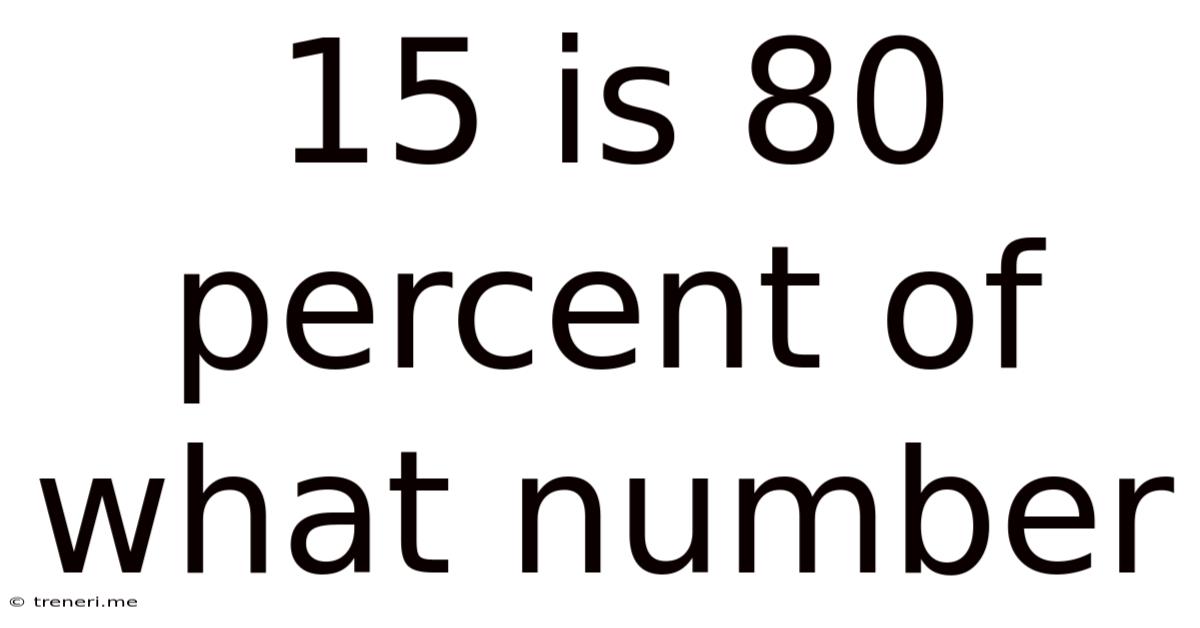
Table of Contents
15 is 80 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analyses. Understanding how to determine the original number when given a percentage and its value is crucial. This article delves into the methods of calculating "15 is 80 percent of what number," exploring multiple approaches and providing a step-by-step guide to mastering similar percentage problems. We'll also cover practical applications and offer tips for improving your percentage calculation skills.
Understanding the Problem: Deconstructing Percentages
Before diving into the solution, let's break down the problem statement: "15 is 80 percent of what number?" This sentence represents a classic percentage problem where we know the resulting value (15) and the percentage (80%), but we need to find the original whole number. This unknown number is often represented by a variable, typically 'x'. The problem can be mathematically expressed as:
15 = 0.80x
This equation forms the basis for our calculations. We'll explore several methods to solve for 'x'.
Method 1: Using the Equation Directly
This is the most straightforward approach. We solve the equation directly by isolating 'x':
-
Convert the percentage to a decimal: 80% is equivalent to 0.80 (divide by 100).
-
Substitute into the equation: 15 = 0.80x
-
Isolate 'x': Divide both sides of the equation by 0.80:
x = 15 / 0.80
-
Calculate: x = 18.75
Therefore, 15 is 80 percent of 18.75.
Method 2: The Proportion Method
This method utilizes proportions to solve for the unknown value. We set up a proportion relating the percentage to the whole:
-
Set up the proportion: We know that 15 represents 80% of the whole number (x). We can write this as a ratio:
15/x = 80/100
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second, and vice versa:
15 * 100 = 80 * x
-
Simplify: This gives us:
1500 = 80x
-
Isolate 'x': Divide both sides by 80:
x = 1500 / 80
-
Calculate: x = 18.75
Again, we arrive at the same solution: 15 is 80 percent of 18.75.
Method 3: Using the Percentage Formula
The percentage formula provides a structured approach to solve various percentage problems. The formula is:
(Part / Whole) * 100% = Percentage
In our case:
- Part = 15
- Percentage = 80%
- Whole = x (unknown)
-
Substitute the known values: (15 / x) * 100% = 80%
-
Simplify: 1500 / x = 80
-
Solve for x: Multiply both sides by x, then divide both sides by 80:
x = 1500 / 80
-
Calculate: x = 18.75
This method reinforces the result: 15 is 80 percent of 18.75.
Practical Applications of Percentage Calculations
The ability to solve percentage problems like "15 is 80 percent of what number" has numerous real-world applications:
-
Finance: Calculating discounts, interest rates, tax amounts, profit margins, and investment returns frequently involves percentage calculations.
-
Retail: Determining the original price of an item after a discount, calculating sales tax, and understanding markups are essential retail skills.
-
Science: Percentage calculations are fundamental in analyzing experimental data, expressing concentrations, and interpreting statistical results.
-
Everyday Life: Calculating tips in restaurants, understanding sales tax, and determining the percentage increase or decrease in prices all utilize percentage concepts.
Tips for Improving Your Percentage Calculation Skills
Mastering percentage calculations requires consistent practice and a clear understanding of the underlying concepts. Here are some helpful tips:
-
Practice Regularly: Solve various percentage problems to build your proficiency. Start with simple problems and gradually increase the complexity.
-
Use Multiple Methods: Familiarize yourself with different approaches, such as the equation method, proportion method, and the percentage formula. This allows you to choose the most efficient method for a given problem.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying logic of percentages and their relationship to fractions and decimals.
-
Check Your Work: Always verify your answers using a different method or by estimating the result.
-
Use Online Resources: Several online calculators and tutorials are available to help you practice and improve your skills. (Note: While we encourage using tools to check answers, relying solely on calculators hinders true understanding.)
-
Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller, more manageable parts.
Expanding Your Knowledge: Beyond Basic Percentages
Understanding the solution to "15 is 80 percent of what number" is a stepping stone to tackling more complex percentage problems. Here are some areas to explore:
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest.
-
Percentage change: Determining the percentage increase or decrease between two values.
-
Percentage points: Understanding the difference between percentage change and percentage points.
-
Weighted averages: Calculating averages where different values have different weights.
Conclusion: Mastering the Art of Percentage Calculations
The ability to accurately solve percentage problems is a vital skill with widespread applications. By understanding the different methods of calculating "15 is 80 percent of what number" and applying the tips provided, you can significantly improve your proficiency in percentage calculations. Remember consistent practice is key to mastering this essential mathematical skill. Continue exploring advanced percentage concepts to broaden your understanding and expand your problem-solving capabilities. With dedication and practice, you'll become confident and proficient in handling various percentage-related challenges in both academic and real-world scenarios.
Latest Posts
Latest Posts
-
Least Common Multiple Of 24 And 9
May 14, 2025
-
How Many Inches Is Approximately 1 M
May 14, 2025
-
The Number 18 Is Which Percent Of 15
May 14, 2025
-
12 X 20 How Many Square Feet
May 14, 2025
-
How Many Square Feet Is A 15 Foot Round Pool
May 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Is 80 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.