16 To The Power Of 2
Treneri
Apr 06, 2025 · 5 min read
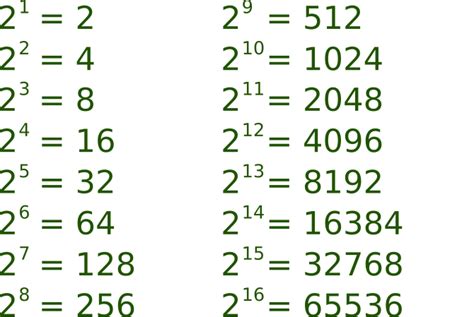
Table of Contents
16 to the Power of 2: Unveiling the Mathematical Magic Behind 16²
The seemingly simple mathematical expression, 16², often gets overlooked. But beneath its unassuming exterior lies a world of mathematical concepts, practical applications, and intriguing connections to other areas of number theory. This comprehensive exploration delves deep into the meaning, calculation, properties, and implications of 16 raised to the power of 2, revealing the surprising depth hidden within this seemingly straightforward calculation.
Understanding Exponents and the Concept of Squaring
Before we dive into the specifics of 16², let's establish a foundational understanding of exponents. An exponent, or power, indicates how many times a number (the base) is multiplied by itself. In the expression x<sup>n</sup>, 'x' represents the base, and 'n' represents the exponent. When the exponent is 2, as in 16², we call this operation "squaring" the number. Squaring a number geometrically represents the area of a square with sides equal to the base number.
Therefore, 16² means 16 multiplied by itself: 16 x 16.
Calculating 16²: Different Approaches
Calculating 16² can be approached in several ways, depending on your preferred method and mathematical proficiency:
1. Direct Multiplication:
The most straightforward method is simply multiplying 16 by itself:
16 x 16 = 256
This method is easily performed manually or using a calculator.
2. Utilizing the Distributive Property (FOIL Method):
We can also view 16 as (10 + 6). Applying the distributive property (often remembered by the acronym FOIL - First, Outer, Inner, Last), we get:
(10 + 6)(10 + 6) = (10 x 10) + (10 x 6) + (6 x 10) + (6 x 6) = 100 + 60 + 60 + 36 = 256
This method demonstrates a deeper understanding of algebraic manipulation and provides a more insightful calculation process.
3. Using the Power of 2 Property:
Recognizing that 16 is 2<sup>4</sup>, we can rewrite 16² as (2<sup>4</sup>)². Using the power of a power rule in exponents ( (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup> ), this simplifies to 2<sup>8</sup>. Then, calculating 2<sup>8</sup>, we get 256. This method showcases the elegant interplay between different exponent rules and simplifies the calculation significantly.
The Significance of 256: Exploring its Properties and Applications
The result of 16², which is 256, holds considerable significance across various fields:
1. Computer Science and Data Representation:
256 (2<sup>8</sup>) plays a crucial role in computer science. It represents the number of distinct values that can be represented by an 8-bit byte. This is foundational to understanding data storage, memory addressing, and color representation in digital images (256 shades of gray or colors in certain color palettes). Understanding the power of 2 is paramount to grasping how computers store and process information.
2. Geometry and Measurement:
As mentioned earlier, squaring a number relates to the area of a square. A square with sides of 16 units has an area of 256 square units. This has implications in various fields, from architecture and construction to land surveying and cartography, where calculating areas is essential.
3. Number Theory and Divisibility:
256, being 2<sup>8</sup>, is highly divisible by powers of 2. Understanding its prime factorization helps in solving number theory problems related to divisibility, factors, and multiples. This knowledge is vital in cryptography and other mathematical applications.
4. Music Theory:
While less apparent, 256 also relates to musical intervals and scales, where powers of 2 are frequently used to define octave relationships and frequency ratios.
Beyond 16²: Expanding on Exponents and Their Applications
The calculation of 16² provides a springboard for exploring more complex exponential relationships. Understanding the concept of squaring extends to other powers (cubing, raising to the fourth power, etc.) and has applications in diverse fields:
- Compound Interest: Calculating compound interest involves exponential growth, where the principal amount increases exponentially over time.
- Population Growth: Modeling population growth often uses exponential functions to describe the increasing population size.
- Exponential Decay: Radioactive decay, the decline in drug concentration in the body, and other natural processes can be modeled using exponential decay functions.
- Scientific Modeling: Exponential functions are crucial in modeling various phenomena in physics, chemistry, biology, and other scientific disciplines.
Advanced Concepts Related to 16² and Exponents
Delving further into the mathematical world, we can explore:
- Logarithms: Logarithms are the inverse of exponential functions. Understanding logarithms allows us to solve equations where the unknown is an exponent. For instance, finding the exponent 'x' in the equation 2<sup>x</sup> = 256 is directly related to the logarithm base 2 of 256.
- Complex Numbers: Exponentiation can extend to complex numbers, leading to fascinating mathematical results and applications in various fields including electrical engineering and quantum mechanics.
- Series and Sequences: Exponential functions are integral parts of various series and sequences, including geometric series, which have numerous applications in mathematics and finance.
Conclusion: The Enduring Relevance of 16²
While the calculation of 16² might initially seem simple, its implications extend far beyond a single mathematical operation. Understanding the concept of squaring, the properties of 256, and the broader applications of exponential functions opens doors to a deeper appreciation of mathematics and its significance across diverse disciplines. From computer science to geometry and beyond, the seemingly simple 16² reveals a rich tapestry of interconnected mathematical concepts and practical applications, highlighting the power and beauty of mathematics. The seemingly trivial calculation reveals itself as a gateway to a wider, more profound understanding of the numerical world. Further exploration of these areas will undoubtedly deepen your appreciation for the elegant and powerful world of mathematics.
Latest Posts
Latest Posts
-
Find The Distance Between Each Pair Of Points Calculator
Apr 06, 2025
-
Cuantos Dias Faltan Para El 15 De Noviembre
Apr 06, 2025
-
Cuanto Es 19 Libras En Kilos
Apr 06, 2025
-
How Long Is A Billion Hours
Apr 06, 2025
-
Cuanto Es 73 Kilos En Libras
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 16 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
