17 Divided By 3 With Remainder
Treneri
May 12, 2025 · 5 min read
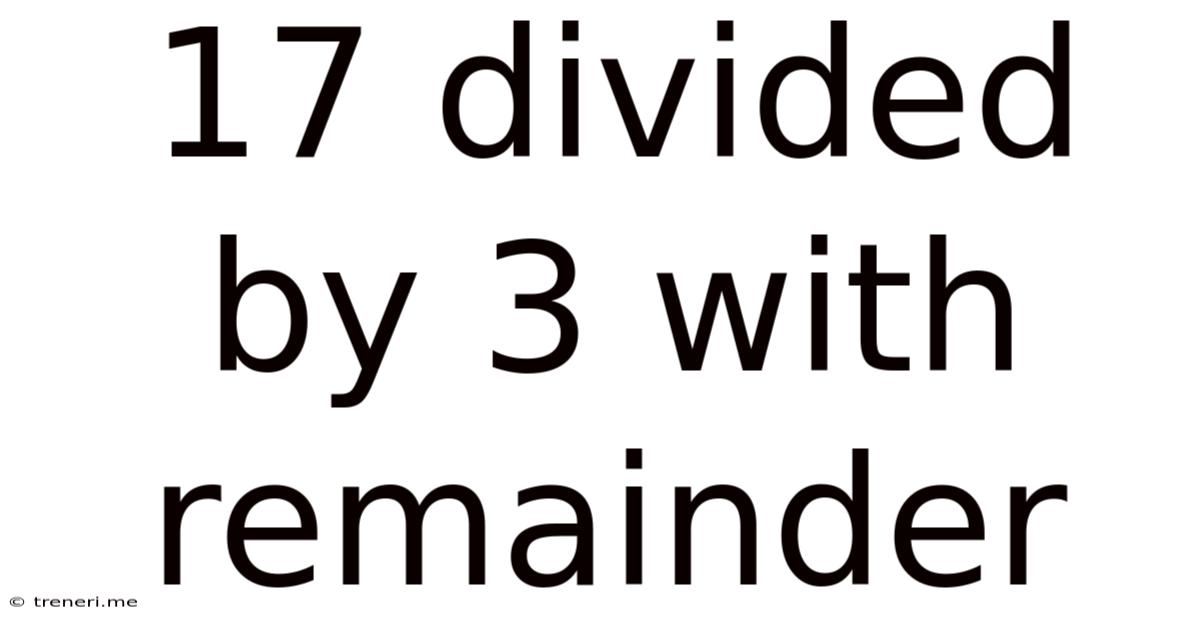
Table of Contents
17 Divided by 3 with Remainder: A Deep Dive into Division and Modular Arithmetic
The seemingly simple question, "What is 17 divided by 3 with remainder?", opens a door to a fascinating world of mathematical concepts. While the answer itself is straightforward (5 with a remainder of 2), exploring the underlying principles reveals the beauty and power of division, particularly within the context of modular arithmetic. This article will delve into this seemingly simple problem, exploring its implications across various mathematical fields and demonstrating its practical applications.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. When we divide 17 by 3, we're essentially asking: "How many times can 3 fit completely into 17?" The answer, in this case, is 5. However, this doesn't fully represent the situation. After fitting 5 groups of 3 into 17 (5 x 3 = 15), we have 2 left over. This leftover amount is called the remainder.
Therefore, 17 divided by 3 can be expressed as:
- 17 ÷ 3 = 5 with a remainder of 2
This can also be represented using the division algorithm:
- Dividend = Quotient x Divisor + Remainder
In our example:
- 17 = 5 x 3 + 2
Where:
- 17 is the dividend (the number being divided).
- 3 is the divisor (the number we're dividing by).
- 5 is the quotient (the result of the division, the whole number part).
- 2 is the remainder (the amount left over).
The Significance of Remainders
Remainders aren't simply leftovers; they hold significant mathematical weight. They're crucial in various areas, including:
1. Modular Arithmetic (Clock Arithmetic)
Modular arithmetic, also known as clock arithmetic, deals with remainders. Think about a 12-hour clock. If it's 10 o'clock and you add 5 hours, the clock doesn't show 15 o'clock; it shows 3 o'clock. This is because 15 modulo 12 (written as 15 mod 12) is 3. The modulo operation gives the remainder after division. In our 17 divided by 3 example, 17 mod 3 = 2.
Modular arithmetic is used extensively in:
- Cryptography: Many encryption algorithms rely heavily on modular arithmetic to ensure data security.
- Computer Science: Hashing functions, used in data structures and databases, often employ modular arithmetic.
- Number Theory: Modular arithmetic forms the foundation for numerous theorems and proofs in number theory.
2. Determining Even and Odd Numbers
The remainder when a number is divided by 2 tells us whether it's even or odd. If the remainder is 0, the number is even; if the remainder is 1, the number is odd. This simple application of remainders is fundamental to many mathematical concepts.
3. Cyclic Patterns and Sequences
Remainders can help identify cyclic patterns in sequences. For instance, consider the remainders when successive powers of 2 are divided by 3:
- 2<sup>1</sup> mod 3 = 2
- 2<sup>2</sup> mod 3 = 1
- 2<sup>3</sup> mod 3 = 2
- 2<sup>4</sup> mod 3 = 1
- ...
The pattern (2, 1) repeats indefinitely. This concept is crucial in understanding periodic functions and sequences.
4. Real-World Applications
Remainders appear frequently in everyday life, often without explicit mention:
- Distributing items: If you have 17 cookies to share among 3 friends, each friend gets 5 cookies, and you have 2 cookies left over.
- Scheduling: Determining the day of the week after a certain number of days often involves modular arithmetic (modulo 7).
- Counting cycles: Analyzing repetitive processes, like machine cycles or daily routines, frequently utilizes remainders to pinpoint patterns or predict future events.
Deeper Dive into the Mathematics
Let's explore some related mathematical concepts:
1. Long Division
Long division is a method for performing division with larger numbers, clearly showing the steps and the remainder. When dividing 17 by 3 using long division, the steps would be:
- How many times does 3 go into 17? 5 times (5 x 3 = 15).
- Subtract 15 from 17, leaving a remainder of 2.
This method visually demonstrates the process and emphasizes the significance of the remainder.
2. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the greatest common divisor (GCD) of two integers. This algorithm relies heavily on the concept of remainders during the division process. For instance, to find the GCD of 17 and 3, we would repeatedly apply the division algorithm:
- 17 = 5 x 3 + 2
- 3 = 1 x 2 + 1
- 2 = 2 x 1 + 0
The last non-zero remainder (1) is the GCD of 17 and 3.
3. Congruences
In modular arithmetic, the statement "a ≡ b (mod m)" means that a and b have the same remainder when divided by m. For example, 17 ≡ 2 (mod 3) because both 17 and 2 have a remainder of 2 when divided by 3. Congruences are a powerful tool for solving problems in number theory and cryptography.
Conclusion: The Unassuming Power of Remainders
The seemingly simple operation of dividing 17 by 3 and finding the remainder unveils a wealth of mathematical concepts. From the fundamentals of division to the sophisticated world of modular arithmetic and the Euclidean algorithm, the remainder plays a vital role. Its applications extend far beyond basic arithmetic, proving indispensable in various fields, including computer science, cryptography, and number theory. Understanding remainders allows us to grasp deeper mathematical structures and appreciate the elegance and practicality of mathematical principles often hidden in plain sight. The next time you encounter a remainder, remember its significant contribution to the vast and interconnected world of mathematics. The seemingly simple "2" in 17 ÷ 3 = 5 R 2 is much more than just a leftover; it's a key that unlocks profound mathematical insights.
Latest Posts
Latest Posts
-
Cuantos Meses Tarda Una Perra En Parir
May 14, 2025
-
Tiempo De Embarazo De Una Perra Pequena
May 14, 2025
-
What Is 40 Percent Of 400
May 14, 2025
-
What Is The Equivalent Fraction Of 9 10
May 14, 2025
-
May 17 2024 How Many Days Away
May 14, 2025
Related Post
Thank you for visiting our website which covers about 17 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.