18 Decreased By 3 Times D
Treneri
May 11, 2025 · 6 min read
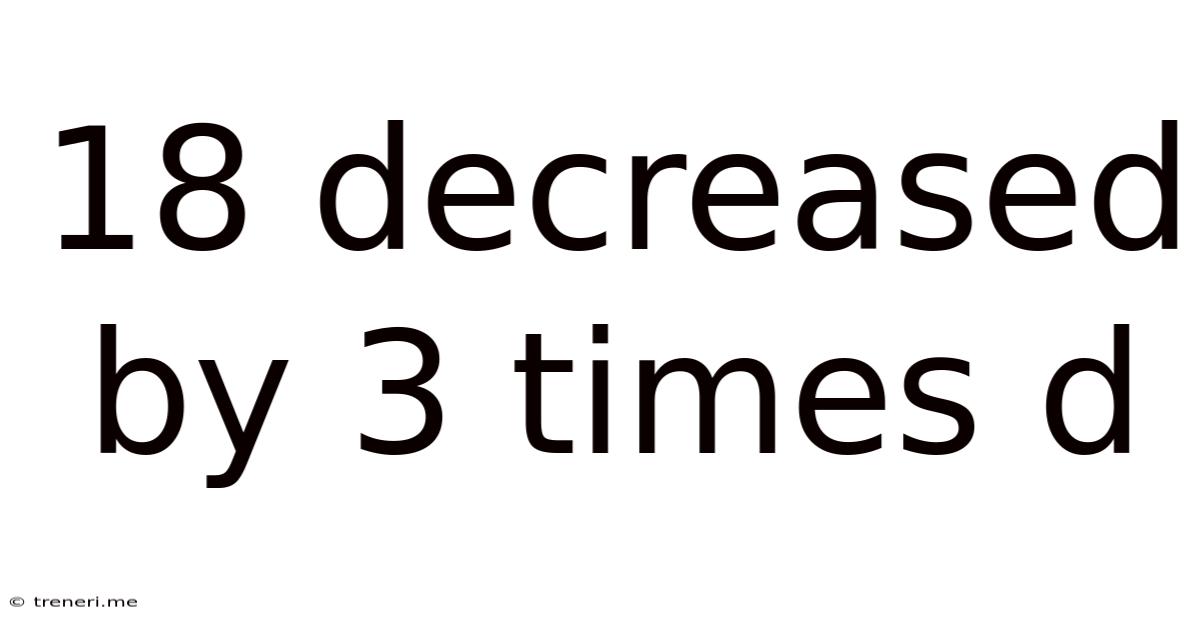
Table of Contents
18 Decreased by 3 Times d: A Comprehensive Exploration of Mathematical Expressions
This article delves into the mathematical expression "18 decreased by 3 times d," exploring its meaning, variations, applications, and potential extensions. We'll unpack the core concept, examining its structure, how to represent it algebraically, and its practical uses in various contexts. We will also discuss related concepts and explore how this seemingly simple expression can be a building block for more complex mathematical problems.
Understanding the Expression: "18 Decreased by 3 Times d"
The phrase "18 decreased by 3 times d" describes a mathematical operation. Let's break it down:
- 18: This is a constant value, a fixed number.
- Decreased by: This indicates subtraction.
- 3 times d: This represents multiplication; '3' is a coefficient, and 'd' is a variable, usually representing an unknown quantity.
Therefore, the entire phrase translates into a mathematical expression: 18 - 3d.
Representing the Expression Algebraically
The algebraic representation, 18 - 3d, is concise and universally understood by mathematicians and anyone working with algebraic equations. This form is crucial for solving problems involving this expression. The variable 'd' allows for flexibility; the expression's value changes depending on the value assigned to 'd'.
Applications and Practical Uses
This simple expression finds application in various scenarios:
1. Geometry and Measurement
Imagine calculating the remaining length of a rope after cutting off several pieces. If you initially had an 18-meter rope and cut off three pieces of equal length ('d' meters each), the remaining length would be represented by 18 - 3d.
2. Finance and Budgeting
Consider a scenario where you have $18 and spend 'd' dollars on three identical items. The money remaining can be modeled using 18 - 3d. This is a fundamental concept in budgeting and financial planning.
3. Physics and Engineering
In physics, this expression might represent the remaining distance after traveling a certain distance multiple times. For example, if an object starts 18 meters away and moves 3d meters closer each time, the remaining distance would be 18 - 3d.
4. Everyday Scenarios
Numerous everyday situations can be modeled using this expression. For example, if you have 18 cookies and share them equally among three friends (each receiving 'd' cookies), the number of cookies left is 18 - 3d.
Solving Equations Involving the Expression
Often, you'll need to solve equations that include this expression. Let's look at some examples:
Example 1: Solve for 'd' if 18 - 3d = 6
- Isolate the term with 'd': Subtract 18 from both sides of the equation: -3d = 6 - 18 = -12
- Solve for 'd': Divide both sides by -3: d = -12 / -3 = 4
Therefore, the solution is d = 4.
Example 2: Solve for 'd' if 18 - 3d = 0
- Isolate the term with 'd': Subtract 18 from both sides: -3d = -18
- Solve for 'd': Divide both sides by -3: d = -18 / -3 = 6
Therefore, the solution is d = 6.
Example 3: If 18 - 3d = 18, what is the value of d?
- Isolate the term with 'd': Subtract 18 from both sides: -3d = 0
- Solve for 'd': Divide both sides by -3: d = 0
Therefore, the solution is d = 0.
These examples illustrate how to solve for 'd' when the expression 18 - 3d is set equal to a specific value. The process involves applying basic algebraic manipulations to isolate the variable.
Exploring Related Concepts and Extensions
The expression "18 decreased by 3 times d" provides a foundation for understanding several related mathematical concepts:
1. Linear Equations
The expression 18 - 3d is a component of linear equations. A linear equation is an equation that can be written in the form y = mx + c, where 'm' is the slope and 'c' is the y-intercept. While our expression doesn't explicitly follow this form, it can be easily manipulated to fit it. For example, if we let y = 18 - 3d, we have a linear equation with a slope of -3 and a y-intercept of 18.
2. Functions
We can express this relationship as a function: f(d) = 18 - 3d. This notation clearly shows that the value of the function (the output) depends on the value of 'd' (the input). This allows us to explore the function's behavior graphically and analytically.
3. Inequalities
The concept can be extended to inequalities. Instead of an equation (e.g., 18 - 3d = 6), we could have an inequality (e.g., 18 - 3d > 6 or 18 - 3d < 6). Solving inequalities requires similar algebraic manipulation, but the solution will be a range of values for 'd', rather than a single value.
4. More Complex Expressions
This simple expression serves as a building block for creating more complex mathematical expressions. For example, we could add another variable or introduce exponents. Understanding the fundamentals of this simpler expression lays the groundwork for tackling more complex mathematical problems.
Real-World Applications and Problem Solving
Let's look at a few more realistic scenarios using the expression:
Scenario 1: Profit Calculation
A small business owner sells handmade crafts. Each craft costs $3 in materials to make. The owner starts with $18. How many crafts ('d') can be made before running out of money?
This translates to the equation: 18 - 3d = 0. Solving this, we find d = 6. Therefore, the owner can make six crafts before running out of money.
Scenario 2: Distance Calculation
A hiker starts 18 kilometers from their destination. They walk 3 kilometers each hour ('d'). How many hours ('d') will it take to reach their destination?
This translates to the equation: 18 - 3d = 0. Solving this, we find d = 6. It will take the hiker six hours to reach their destination.
Scenario 3: Temperature Change
The temperature is 18 degrees Celsius. The temperature decreases by 3 degrees Celsius per hour ('d'). After how many hours ('d') will the temperature reach 6 degrees Celsius?
This translates to the equation: 18 - 3d = 6. Solving this, we find d = 4. The temperature will reach 6 degrees Celsius after four hours.
These examples highlight the practical applications of the expression in various real-world situations, emphasizing its usefulness in problem-solving.
Conclusion
The seemingly simple expression "18 decreased by 3 times d," represented algebraically as 18 - 3d, holds significant value in mathematics and its applications. Understanding its structure, how to manipulate it algebraically, and its practical applications in diverse fields, from finance to physics, is crucial. This article explored its fundamental aspects and highlighted its role as a building block for more complex mathematical concepts and problem-solving. Mastering this fundamental expression solidifies a strong foundation for tackling more advanced mathematical challenges.
Latest Posts
Latest Posts
-
120 Days From May 20 2024
May 12, 2025
-
1 1 3 As An Improper Fraction
May 12, 2025
-
2420 Rounded To The Nearest Ten
May 12, 2025
-
How Many Psi Is One Bar
May 12, 2025
-
0 3 To The Power Of 2
May 12, 2025
Related Post
Thank you for visiting our website which covers about 18 Decreased By 3 Times D . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.