18 Is 30 Percent Of What Number
Treneri
May 09, 2025 · 5 min read
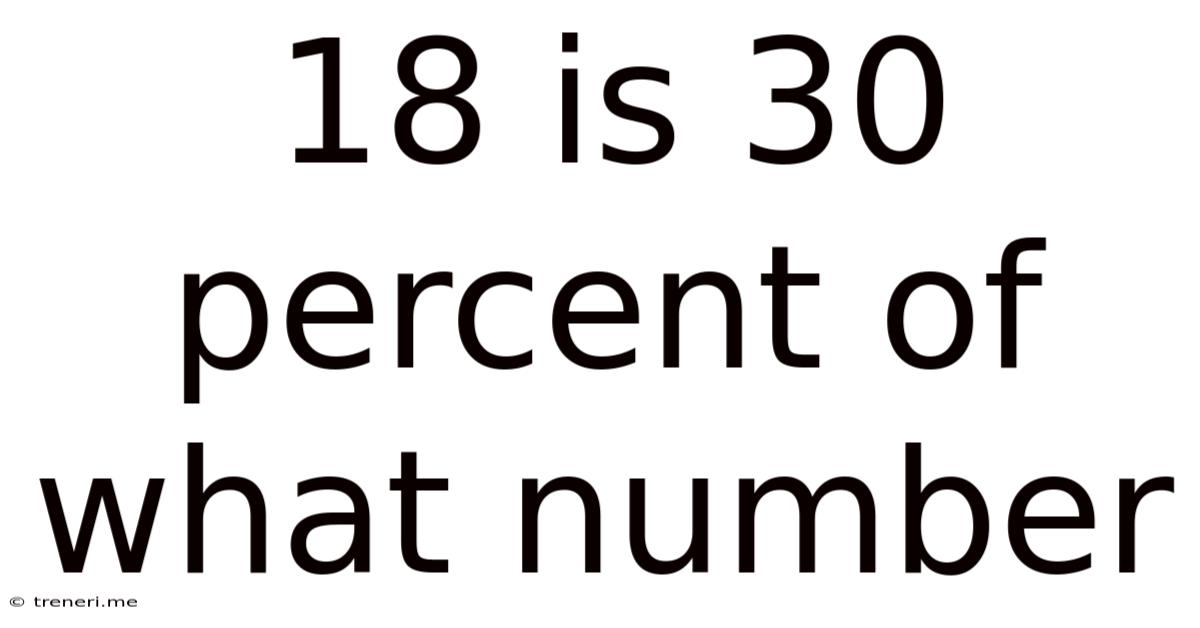
Table of Contents
18 is 30 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the question, "18 is 30 percent of what number?" We'll not only solve this specific problem but also explore the broader concepts of percentages, providing you with a comprehensive understanding and equipping you with the tools to solve similar percentage problems independently.
Understanding Percentages: The Basics
Before diving into the problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred," indicating a ratio of a number to 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Terms:
- Percentage: The portion of a whole expressed as a number out of 100.
- Base: The total amount or the whole value. This is the number we're finding a percentage of.
- Part: The portion of the base that represents the percentage.
Solving "18 is 30 Percent of What Number?"
Now, let's tackle our core problem: "18 is 30 percent of what number?" We can represent this problem mathematically as follows:
18 = 30% * x
Where 'x' represents the unknown number we're trying to find.
Method 1: Using the Equation
To solve for 'x', we can rearrange the equation:
x = 18 / (30/100)
This simplifies to:
x = 18 / 0.3
Therefore:
x = 60
Thus, 18 is 30 percent of 60.
Method 2: Proportion Method
Another approach is using proportions. We can set up a proportion as follows:
18/x = 30/100
Cross-multiplying, we get:
18 * 100 = 30 * x
1800 = 30x
Dividing both sides by 30:
x = 1800 / 30
x = 60
Again, we find that 18 is 30 percent of 60.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in a wide range of real-world scenarios. Here are a few examples:
1. Calculating Discounts:
Imagine a store offers a 20% discount on an item originally priced at $80. To find the discounted price, we calculate 20% of $80:
0.20 * $80 = $16
The discount is $16, so the final price is $80 - $16 = $64.
2. Determining Tax Amounts:
Sales tax is often expressed as a percentage. If the sales tax is 6% and the pre-tax price of an item is $50, the tax amount is:
0.06 * $50 = $3
The total price, including tax, is $50 + $3 = $53.
3. Analyzing Financial Statements:
Percentage calculations are essential for analyzing financial data. For instance, understanding the percentage change in revenue or profit from one period to another provides valuable insights into a company's financial performance. A 10% increase in revenue signifies strong growth, while a 5% decrease indicates a decline.
4. Understanding Statistics and Data:
Percentages are frequently used to represent data in surveys, polls, and research studies. For example, a survey may show that 75% of respondents prefer a particular product. This percentage helps in drawing conclusions and making data-driven decisions.
5. Calculating Interest Rates:
Interest rates on loans, savings accounts, and investments are typically expressed as percentages. Understanding how to calculate interest earned or paid is vital for personal finance management. The formula for simple interest is:
Interest = Principal * Rate * Time
Where the 'rate' is expressed as a percentage.
Beyond the Basics: More Complex Percentage Problems
While the problem "18 is 30 percent of what number?" is relatively straightforward, percentage calculations can become more complex. Here are a few examples of more advanced scenarios:
1. Calculating Percentage Increase or Decrease:
Determining the percentage change between two values requires a slightly different approach. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
For instance, if sales increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] * 100 = 20%
2. Working with Multiple Percentages:
Problems involving successive percentages, such as calculating discounts after applying a coupon and then a sales tax, require careful attention to order of operations. You must apply the percentages sequentially.
3. Solving Problems with Unknown Variables:
Many real-world scenarios involve more than one unknown variable. These problems often require using algebraic equations to find solutions.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips to improve your proficiency in percentage calculations:
- Practice Regularly: The key to mastering any mathematical concept is consistent practice. Solve various percentage problems to build your confidence and understanding.
- Use Different Methods: Experiment with different methods like the equation method and the proportion method to find the approach that suits you best.
- Break Down Complex Problems: Simplify complex problems by breaking them into smaller, more manageable steps.
- Check Your Work: Always double-check your calculations to ensure accuracy. Using a calculator can help avoid simple arithmetic errors.
- Understand the Context: Pay close attention to the context of the problem to ensure you're applying the correct formula or method.
Conclusion: The Power of Percentage Understanding
The ability to solve percentage problems, even seemingly simple ones like "18 is 30 percent of what number?", is a valuable asset. This skill is widely applicable in various aspects of daily life, from shopping and budgeting to analyzing data and making informed decisions. By mastering the fundamentals and practicing regularly, you can confidently tackle a wide range of percentage calculations and unlock the power of numerical literacy. Remember to break down complex problems, practice consistently, and always check your work for accuracy. With dedication and practice, you can become proficient in the art of percentage calculations.
Latest Posts
Latest Posts
-
Foot Is 10 Inches What Shoe Size
May 10, 2025
-
How Many Years Is 95 Months
May 10, 2025
-
1 60 De Altura Nos Eua
May 10, 2025
-
Your Base Salary Is 20000 You Receive 5 Commission
May 10, 2025
-
How Many Cups In A Lint
May 10, 2025
Related Post
Thank you for visiting our website which covers about 18 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.