18 Is What Percentage Of 30
Treneri
May 12, 2025 · 4 min read
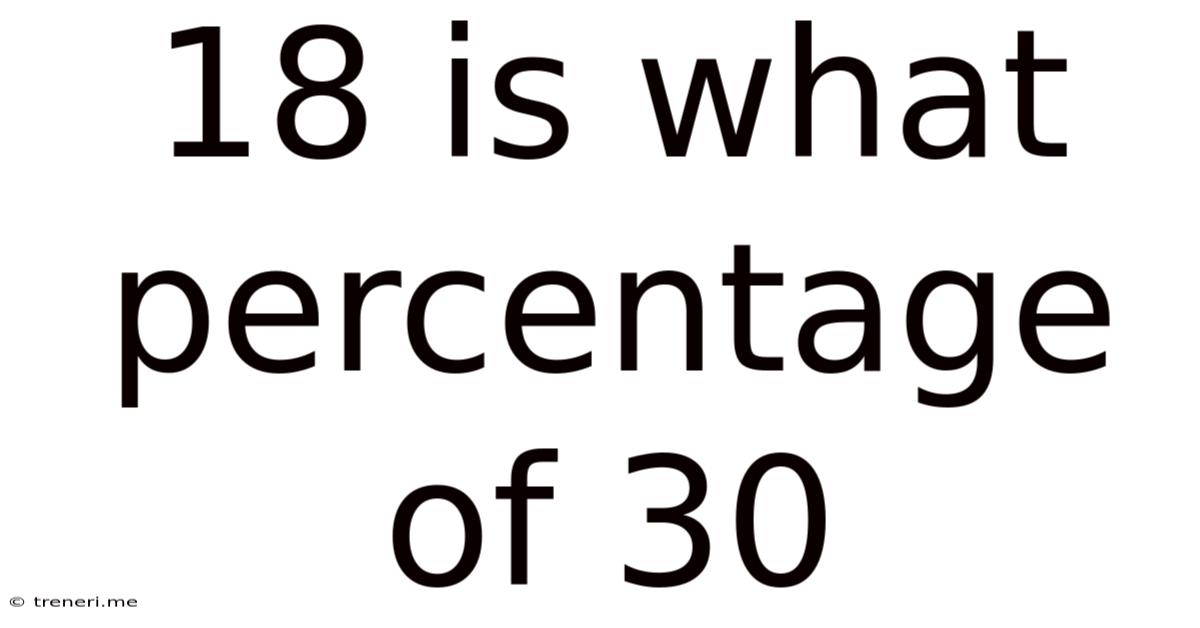
Table of Contents
18 is What Percentage of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and sales tax to analyzing data and understanding financial reports. This article delves into the question, "18 is what percentage of 30?", providing a comprehensive explanation of the calculation process, practical applications, and related percentage problems. We'll explore different methods of solving this type of problem, ensuring you gain a solid understanding of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol used to represent percentage is "%". Essentially, it shows the proportion of one number relative to another. For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Key Concepts:
- Part: The number representing a portion of the whole. In our example, 18 is the part.
- Whole: The total number or the complete amount. In our example, 30 is the whole.
- Percentage: The proportion of the part relative to the whole, expressed as a percentage. This is what we need to calculate.
Calculating "18 is What Percentage of 30?"
There are several methods to solve this problem:
Method 1: Using the Formula
The fundamental formula for calculating percentage is:
(Part / Whole) x 100% = Percentage
Applying this to our problem:
(18 / 30) x 100% = 0.6 x 100% = 60%
Therefore, 18 is 60% of 30.
Method 2: Using Proportions
We can set up a proportion to solve this:
18/30 = x/100
Where 'x' represents the percentage we need to find. To solve for x, we cross-multiply:
30x = 1800
x = 1800 / 30
x = 60
Therefore, x = 60%, confirming our previous result.
Method 3: Using Decimal Conversion
First, we express the part as a fraction of the whole:
18/30 = 0.6
Then, we convert this decimal to a percentage by multiplying by 100%:
0.6 x 100% = 60%
Practical Applications of Percentage Calculations
Understanding percentage calculations has wide-ranging applications in various real-world scenarios. Here are some examples:
1. Sales and Discounts:
Imagine a shirt originally priced at $30 is on sale for $18. Using the methods outlined above, we can determine that the discount is 60%. This is crucial information for consumers to compare prices and make informed decisions. Retailers also use percentage calculations extensively for profit margins, markups, and clearance sales.
2. Financial Calculations:
Percentages are essential in finance. Interest rates on loans and savings accounts are expressed as percentages. Calculating interest earned or owed, understanding APR (Annual Percentage Rate), and analyzing investment returns all rely heavily on percentage calculations.
3. Data Analysis and Statistics:
In statistics and data analysis, percentages are used to represent proportions within datasets. For example, if a survey shows that 18 out of 30 people prefer a particular brand, we can represent this as 60% preference. This helps in summarizing and interpreting large datasets.
4. Grade Calculations:
In education, percentages are frequently used to represent grades. If a student scores 18 out of 30 points on a test, their score is 60%. This allows for a standardized way of representing academic performance.
5. Tax Calculations:
Sales tax, income tax, and other taxes are often expressed as percentages of the taxable amount. Understanding these percentages is critical for budgeting and financial planning.
Solving Related Percentage Problems
Let's explore some related percentage problems to further solidify your understanding:
Problem 1: What is 25% of 80?
Using the formula: (25/100) x 80 = 20
Problem 2: If 15 is 30% of a number, what is the number?
Let 'x' be the number. Then:
(30/100) x x = 15
0.3x = 15
x = 15 / 0.3
x = 50
Problem 3: A store offers a 15% discount on an item priced at $60. What is the discounted price?
Discount amount = (15/100) x 60 = $9
Discounted price = $60 - $9 = $51
Problem 4: Increase 45 by 20%.
Increase amount = (20/100) x 45 = 9
New value = 45 + 9 = 54
Advanced Percentage Concepts
While the examples above focus on straightforward calculations, percentages can be used in more complex scenarios:
- Compound interest: Interest calculated not only on the principal but also on accumulated interest.
- Percentage change: Calculating the increase or decrease in a value over time.
- Percentage point difference: Representing the difference between two percentages.
Conclusion
The ability to calculate percentages accurately is a valuable skill with applications in many areas of life. This article has provided a comprehensive guide to solving percentage problems, specifically addressing "18 is what percentage of 30?". By understanding the fundamental formula and different calculation methods, you can confidently tackle a wide range of percentage-related challenges and apply this knowledge effectively in various contexts. Remember to practice regularly to reinforce your understanding and improve your proficiency in this essential mathematical skill. Mastering percentage calculations will empower you to analyze data more effectively, make sound financial decisions, and navigate everyday situations with greater confidence.
Latest Posts
Latest Posts
-
90 Out Of 100 As A Percentage
May 13, 2025
-
How Much Is 119 Grams In Cups
May 13, 2025
-
Cuantos Meses Hay En Un Ano
May 13, 2025
-
What Is 6 9 107 Written In Standard Form
May 13, 2025
-
998 Rounded To The Nearest Ten
May 13, 2025
Related Post
Thank you for visiting our website which covers about 18 Is What Percentage Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.