2 3 Divided By 1 2 In Fraction
Treneri
May 09, 2025 · 6 min read
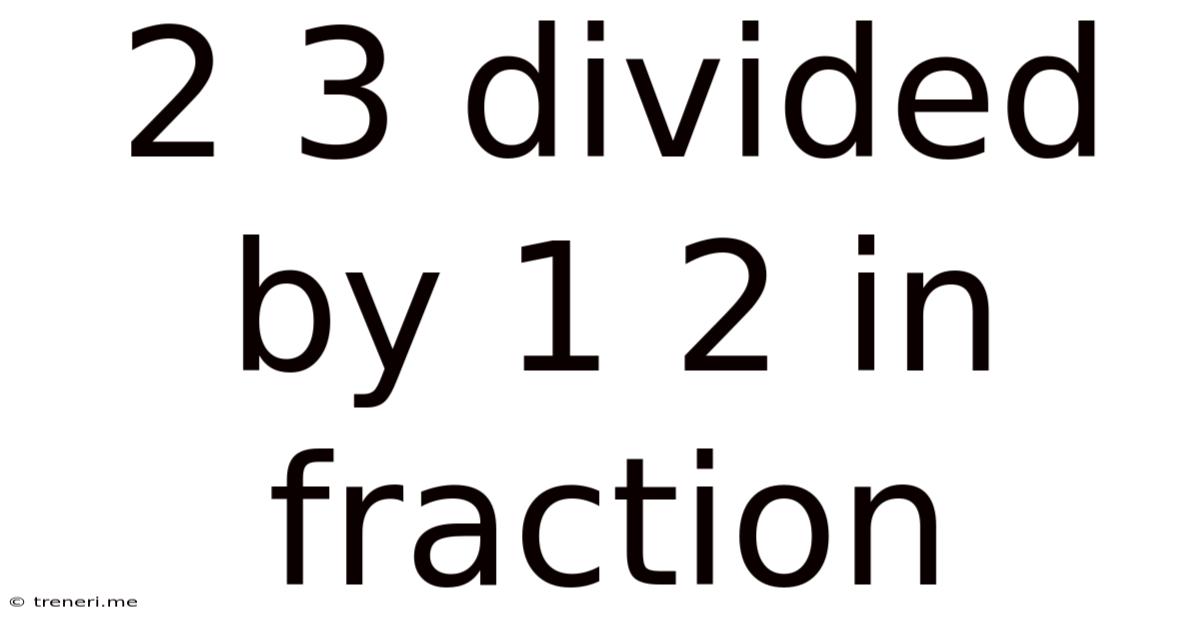
Table of Contents
2/3 Divided by 1/2: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through dividing 2/3 by 1/2, explaining the underlying principles and offering various approaches to solve this type of problem. We'll explore the "keep, change, flip" method, the reciprocal method, and delve into the conceptual understanding behind fraction division. By the end, you'll be confident in tackling similar fraction division problems.
Understanding Fraction Division
Before jumping into the calculation of 2/3 divided by 1/2, let's establish a solid foundation in fraction division. What does it mean to divide a fraction by another fraction? Fundamentally, it's asking: "How many times does one fraction fit into another?"
For instance, 2/3 divided by 1/2 asks: "How many times does 1/2 fit into 2/3?" This question might seem abstract initially, but visualizing it can help. Imagine you have a pizza cut into three slices. You have two of those slices (2/3 of the pizza). Now, you want to know how many times you can take a half slice (1/2) from your 2/3 portion.
Method 1: The "Keep, Change, Flip" Method (or Invert and Multiply)
This is arguably the most popular method for dividing fractions. It's a simple three-step process:
- Keep: Keep the first fraction exactly as it is. In our example, this is 2/3.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (find the reciprocal of) the second fraction. The reciprocal of 1/2 is 2/1 (or simply 2).
Let's apply this to our problem:
2/3 ÷ 1/2 becomes 2/3 × 2/1
Now, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(2 × 2) / (3 × 1) = 4/3
Therefore, 2/3 divided by 1/2 equals 4/3. This can also be expressed as a mixed number: 1 1/3.
Visualizing the Result
Let's revisit our pizza analogy. We had 2/3 of a pizza, and we wanted to know how many 1/2 slices we could get. Our answer, 4/3 or 1 1/3, means we can get one and a third half-slices from our 2/3 portion.
Method 2: The Reciprocal Method
This method is essentially the same as "keep, change, flip," but it emphasizes the concept of reciprocals. A reciprocal is simply a fraction flipped upside down. To divide by a fraction, we multiply by its reciprocal.
So, 2/3 ÷ 1/2 is equivalent to 2/3 × 2/1 (the reciprocal of 1/2). The calculation remains the same as in the previous method, yielding the answer 4/3 or 1 1/3.
Why Does "Keep, Change, Flip" Work?
The "keep, change, flip" method isn't just a trick; it's a consequence of the rules of fraction division and multiplication. To understand this, let's consider the division of any two fractions a/b and c/d:
(a/b) ÷ (c/d)
We can rewrite this division as a complex fraction:
(a/b) / (c/d)
To simplify a complex fraction, we multiply the numerator by the reciprocal of the denominator:
(a/b) × (d/c) = (a × d) / (b × c)
Notice that this is precisely what the "keep, change, flip" method does. It's a shortcut that streamlines the process of simplifying complex fractions.
Working with Mixed Numbers
Sometimes, you might encounter mixed numbers in fraction division problems. For example, let's say we need to calculate 1 1/2 ÷ 2/3.
Before applying the "keep, change, flip" method, we must first convert the mixed number (1 1/2) into an improper fraction. To do this, multiply the whole number (1) by the denominator (2) and add the numerator (1). This sum (3) becomes the new numerator, while the denominator remains the same (2). Thus, 1 1/2 becomes 3/2.
Now, we can apply the "keep, change, flip" method:
3/2 ÷ 2/3 becomes 3/2 × 3/2 = 9/4 or 2 1/4
Solving More Complex Problems
The principles discussed above apply to all fraction division problems, regardless of complexity. Let's try a more challenging example: (5/8) ÷ (3/4)
- Keep: Keep the first fraction: 5/8
- Change: Change the division sign to multiplication: ×
- Flip: Flip the second fraction: 4/3
Now, multiply:
(5/8) × (4/3) = (5 × 4) / (8 × 3) = 20/24
We can simplify this fraction by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 4:
20/24 = (20 ÷ 4) / (24 ÷ 4) = 5/6
Therefore, (5/8) ÷ (3/4) = 5/6.
Practical Applications of Fraction Division
Fraction division is more than just a mathematical exercise; it has many practical applications in everyday life and various fields. Here are some examples:
- Cooking and Baking: Scaling recipes up or down often requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make only half the recipe, you'll need to divide 1/2 by 2.
- Sewing and Tailoring: Calculating fabric requirements often involves fraction division. If you need a certain length of fabric and have a specific width, determining the number of pieces you need involves fractions.
- Construction and Engineering: Dividing fractions is crucial in accurate measurements and calculations in construction projects.
- Finance and Budgeting: Dividing fractions can be helpful in splitting bills or calculating proportions of a budget.
Troubleshooting Common Mistakes
Even with a clear understanding of the process, some common mistakes can occur when dividing fractions:
- Forgetting to flip the second fraction: This is a very common error. Remember the "keep, change, flip" rule meticulously.
- Incorrectly multiplying or simplifying fractions: Double-check your multiplication and simplification steps to avoid errors.
- Not converting mixed numbers to improper fractions: Always convert mixed numbers to improper fractions before performing the division.
Conclusion
Dividing fractions, while initially appearing complex, is a manageable skill once the underlying principles are understood. The "keep, change, flip" method provides a simple and effective way to solve these problems. By mastering this technique and understanding the conceptual basis of fraction division, you'll be well-equipped to handle a wide range of mathematical problems in various contexts, both academic and practical. Remember to practice regularly to build confidence and proficiency. With consistent effort, fraction division will become second nature.
Latest Posts
Latest Posts
-
Weight Of 1 Pint Of Water
May 09, 2025
-
Cuanto Es 1 M En Pies
May 09, 2025
-
Finding An Exponential Function Given Two Points
May 09, 2025
-
How Many Minutes Is A Mile Driving
May 09, 2025
-
Greatest Common Factor Of 42 And 48
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 1 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.