2 3 Divided By 1 2 In Fraction Form
Treneri
May 14, 2025 · 5 min read
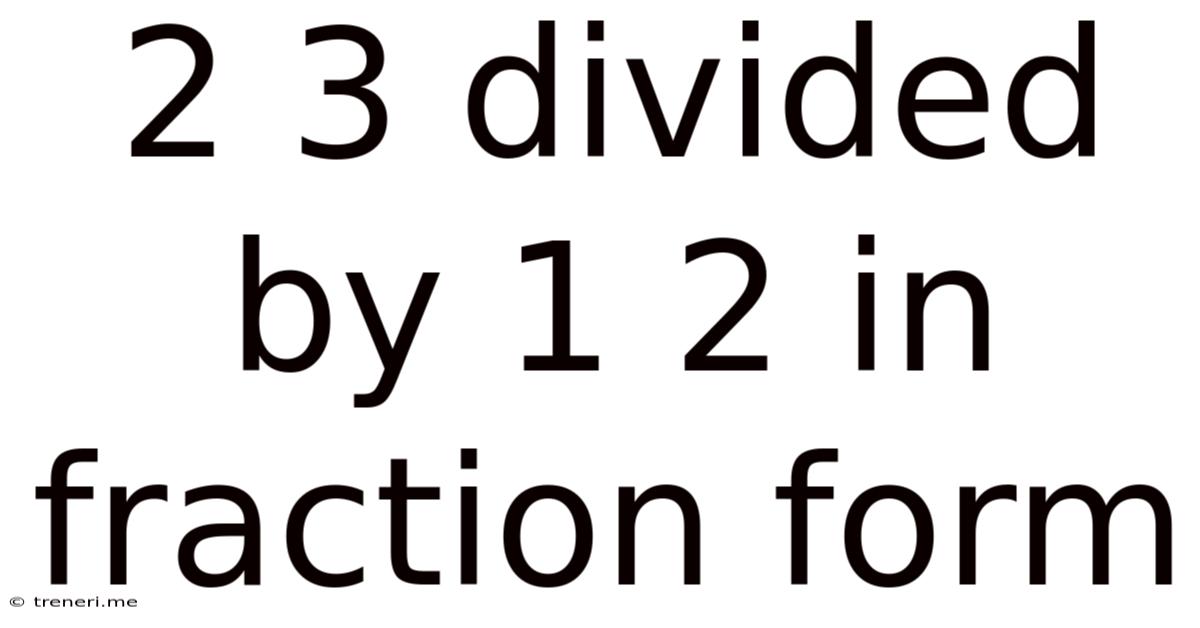
Table of Contents
2/3 Divided by 1/2 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 2/3 by 1/2, explaining the concept thoroughly and providing numerous examples to solidify your understanding. We'll explore different methods, delve into the underlying mathematical principles, and offer tips for tackling similar fraction division problems.
Understanding Fraction Division
Before diving into the specific problem of 2/3 divided by 1/2, let's establish a solid foundation in fraction division. The key concept to grasp is that dividing by a fraction is the same as multiplying by its reciprocal.
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/2 is 2/1 (or simply 2). The reciprocal of 3/4 is 4/3, and the reciprocal of 5/7 is 7/5.
This crucial understanding forms the basis of our approach to solving 2/3 ÷ 1/2.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing fractions. To divide 2/3 by 1/2, we follow these steps:
-
Find the reciprocal of the second fraction (the divisor): The reciprocal of 1/2 is 2/1.
-
Change the division sign to a multiplication sign: Our problem now becomes 2/3 x 2/1.
-
Multiply the numerators (top numbers) together: 2 x 2 = 4
-
Multiply the denominators (bottom numbers) together: 3 x 1 = 3
-
Simplify the resulting fraction (if possible): In this case, 4/3 is already in its simplest form.
Therefore, 2/3 ÷ 1/2 = 4/3. This can also be expressed as a mixed number: 1 1/3.
Method 2: Using a Common Denominator
While the reciprocal method is generally preferred for its simplicity, we can also solve this using a common denominator. This method is more helpful in understanding the underlying principles of fraction division, particularly for those still developing their fractional understanding.
-
Find a common denominator for both fractions: The least common denominator for 3 and 2 is 6.
-
Convert both fractions to equivalent fractions with the common denominator:
- 2/3 becomes 4/6 (multiply both numerator and denominator by 2)
- 1/2 becomes 3/6 (multiply both numerator and denominator by 3)
-
Rewrite the division problem: The problem becomes 4/6 ÷ 3/6.
-
Divide the numerators: 4 ÷ 3 = 4/3
-
The denominators cancel out: Since the denominators are the same, they effectively cancel each other out.
Therefore, we arrive at the same answer: 4/3 or 1 1/3.
Illustrative Examples
Let's apply the reciprocal method to a few more examples to solidify our understanding:
-
Example 1: 3/4 ÷ 2/5
- Reciprocal of 2/5 is 5/2
- 3/4 x 5/2 = 15/8 (This can be expressed as 1 7/8)
-
Example 2: 1/3 ÷ 1/6
- Reciprocal of 1/6 is 6/1
- 1/3 x 6/1 = 6/3 = 2
-
Example 3: 5/8 ÷ 1/4
- Reciprocal of 1/4 is 4/1
- 5/8 x 4/1 = 20/8 = 5/2 (This can be expressed as 2 1/2)
These examples highlight the consistent application of the reciprocal method.
Why the Reciprocal Method Works
The reciprocal method works because division is fundamentally the inverse operation of multiplication. When we divide by a fraction, we're essentially asking "How many times does this fraction fit into the other fraction?" Multiplying by the reciprocal is a mathematical shortcut that elegantly answers this question.
Consider the problem 2/3 ÷ 1/2 visually. Imagine dividing a rectangle into thirds and then further dividing each third in half. You end up with six smaller sections, and the fraction 2/3 now represents 4 out of those 6 sections (4/6). Since each section is 1/2 of a third, it becomes clear that 2/3 contains 4/3 of 1/2. This visualization aligns perfectly with the outcome of our mathematical approach.
Tackling More Complex Problems
The principles discussed here can be extended to more complex problems involving mixed numbers or more than two fractions. For problems involving mixed numbers, always convert the mixed numbers into improper fractions before applying the reciprocal method. For problems with multiple fractions, work through them step by step, following the order of operations (PEMDAS/BODMAS).
Practical Applications of Fraction Division
Fraction division is not merely an abstract mathematical concept; it finds widespread application in numerous real-world scenarios. From calculating ingredient ratios in cooking to determining the number of tiles needed for a floor, understanding fraction division is essential for efficient and accurate problem-solving. In construction, tailoring garments, and many other trades, the ability to accurately manipulate fractions is vital.
Common Mistakes to Avoid
While fraction division is relatively straightforward, some common mistakes can lead to incorrect answers.
- Forgetting to find the reciprocal: Remember, the crucial step is to flip the second fraction (the divisor) before multiplying.
- Incorrect multiplication: Pay attention to the rules of multiplying fractions—multiply numerators and denominators separately.
- Failing to simplify: Always simplify your answer to the lowest terms to present a concise and accurate solution.
Conclusion
Dividing fractions, especially a problem like 2/3 divided by 1/2, becomes manageable with a solid grasp of the reciprocal method. By understanding the underlying principle and practicing consistently, you'll build confidence in tackling even more complex fraction division problems. Remember to convert mixed numbers to improper fractions, simplify your answers, and double-check your work to avoid common errors. With practice and a clear understanding, fraction division will cease to be a challenge and become a valuable tool in your mathematical arsenal. The answer, 4/3 or 1 1/3, is a testament to the power and elegance of fractional arithmetic.
Latest Posts
Latest Posts
-
What Is 40 Percent Off Of 45 Dollars
May 14, 2025
-
How To Measure Gallons Of Water In A Pond
May 14, 2025
-
949 Rounded To The Nearest Hundred
May 14, 2025
-
Time And A Half For 16
May 14, 2025
-
Real Estate Agent Commission On Rental
May 14, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 1 2 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.