2/5 + 1/4 As A Fraction
Treneri
May 12, 2025 · 6 min read
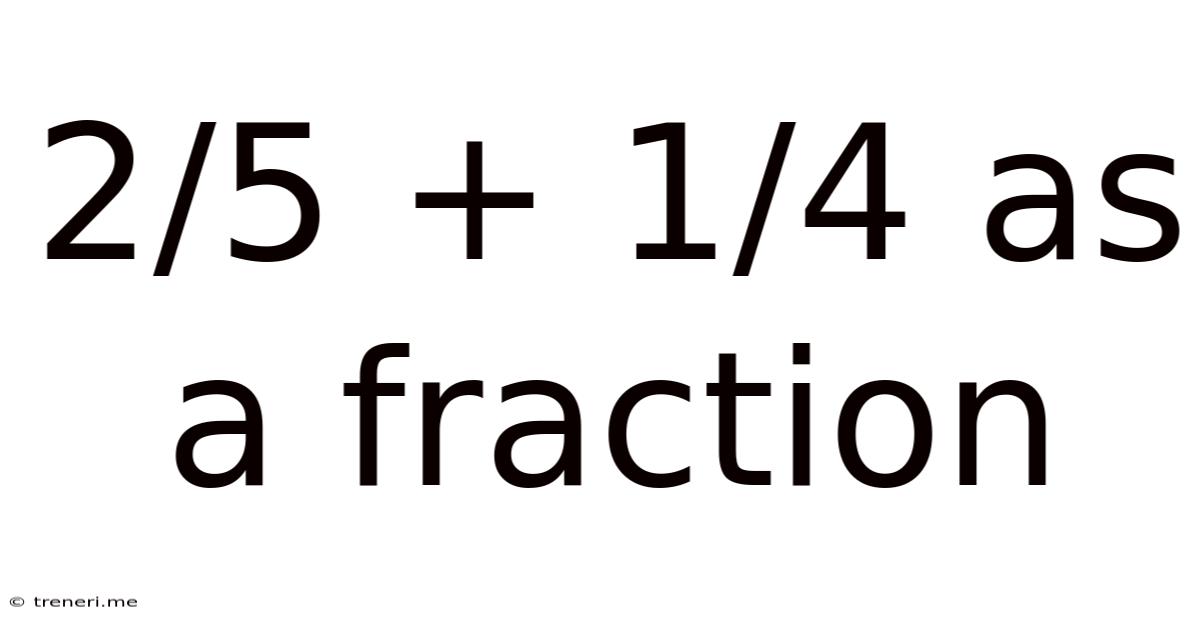
Table of Contents
2/5 + 1/4 as a Fraction: A Comprehensive Guide to Adding Fractions
Adding fractions might seem daunting at first, but with a structured approach and a good understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through adding 2/5 and 1/4, explaining the concepts in detail and providing practical examples to solidify your understanding. We'll explore different methods, address common mistakes, and delve into the broader application of adding fractions in various mathematical contexts.
Understanding Fractions: A Quick Recap
Before tackling the addition of 2/5 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 2/5, the numerator (2) represents two parts, and the denominator (5) means the whole is divided into five equal parts.
Why We Need a Common Denominator
Adding fractions directly, without considering their denominators, is incorrect. Imagine trying to add apples and oranges – you can't simply say you have "3" without specifying whether you have three apples, three oranges, or a combination. Similarly, the denominators of fractions represent the "type" of part we're dealing with. To add them, we need to ensure they are the same "type"—this is achieved by finding a common denominator.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find the smallest number that appears in both lists. For 5 and 4, the multiples are:
- Multiples of 5: 5, 10, 15, 20, 25...
- Multiples of 4: 4, 8, 12, 16, 20, 24... The smallest common multiple is 20.
-
Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in the denominators. For 5 and 4:
- 5 = 5
- 4 = 2 x 2 = 2² Therefore, the LCD = 2² x 5 = 20
Converting Fractions to Equivalent Fractions
Once we have the LCD (which is 20 in this case), we need to convert both fractions (2/5 and 1/4) into equivalent fractions with the denominator of 20. This means we need to find a number to multiply both the numerator and denominator of each fraction to obtain the LCD.
-
For 2/5: To get a denominator of 20, we multiply the denominator (5) by 4. To maintain the value of the fraction, we must also multiply the numerator by 4: (2 x 4) / (5 x 4) = 8/20
-
For 1/4: To get a denominator of 20, we multiply the denominator (4) by 5. Again, we must also multiply the numerator by 5: (1 x 5) / (4 x 5) = 5/20
Adding the Fractions
Now that both fractions have the same denominator (20), we can add them:
8/20 + 5/20 = (8 + 5) / 20 = 13/20
Therefore, 2/5 + 1/4 = 13/20
Simplifying Fractions (If Necessary)
In this case, 13/20 is already in its simplest form because 13 and 20 share no common factors other than 1. If the resulting fraction had a common factor in the numerator and denominator, we would simplify it by dividing both by their greatest common divisor (GCD).
Alternative Methods: Using Decimal Representation
While the common denominator method is generally preferred for its accuracy and conceptual clarity, you can also add fractions using their decimal equivalents. However, this method sometimes results in approximations, especially with fractions that produce non-terminating decimals.
-
Convert to Decimals:
- 2/5 = 0.4
- 1/4 = 0.25
-
Add Decimals:
- 0.4 + 0.25 = 0.65
-
Convert back to a Fraction (if needed): Converting 0.65 back to a fraction involves writing it as 65/100 and then simplifying by dividing both numerator and denominator by their GCD (5): 65/100 = 13/20.
Real-World Applications of Adding Fractions
Adding fractions is not just a theoretical exercise; it's a crucial skill applicable in numerous real-world scenarios:
-
Cooking and Baking: Recipes often involve fractional measurements of ingredients. Adding fractions helps determine the total amount of an ingredient needed.
-
Construction and Engineering: Precise measurements are essential in construction. Adding fractions allows for accurate calculations of lengths, areas, and volumes.
-
Finance: Dealing with portions of money, calculating interest, and managing budgets all involve fractional arithmetic.
-
Data Analysis: In various fields, data is often represented as fractions or percentages. Adding fractions helps in combining and interpreting data sets.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect answers when adding fractions:
-
Adding numerators and denominators directly: This is a fundamental error. Remember, you must find a common denominator before adding the numerators.
-
Incorrectly finding the LCD: Using an incorrect LCD will result in an inaccurate sum. Double-check your calculations when finding the LCD.
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms to present the answer in its most concise form.
Advanced Concepts and Extensions
While adding simple fractions like 2/5 and 1/4 is relatively straightforward, the principles can be extended to more complex scenarios:
-
Adding mixed numbers: Mixed numbers consist of a whole number and a fraction (e.g., 1 1/2). To add mixed numbers, you first convert them to improper fractions, find a common denominator, add the fractions, and then convert the result back to a mixed number if needed.
-
Adding more than two fractions: The process remains similar; find the LCD for all the denominators, convert the fractions to equivalent fractions with the LCD, and then add the numerators.
-
Adding fractions with variables: Algebraic fractions involve variables in the numerator and/or denominator. The principles of finding a common denominator and adding fractions remain the same, though algebraic manipulation may be required.
Conclusion
Adding fractions, even seemingly simple ones like 2/5 + 1/4, involves a methodical approach that necessitates understanding the concept of common denominators and equivalent fractions. Mastering these fundamental concepts allows for accurate calculations and opens up the possibility of applying fractional arithmetic to a wide range of practical problems in various domains. By avoiding common pitfalls and practicing regularly, you can build confidence and proficiency in this crucial mathematical skill. Remember, the key is to understand why you're performing each step, not just how to perform it. This understanding will serve you well as you progress to more complex mathematical concepts.
Latest Posts
Latest Posts
-
Cuantos Dias Faltan Para El 15 De Enero
May 12, 2025
-
50 Rounded To The Nearest Ten
May 12, 2025
-
Is 4 5 Equal To 8 10
May 12, 2025
-
How Much Days Until June 1st
May 12, 2025
-
How Long Should It Take To Read 30 Pages
May 12, 2025
Related Post
Thank you for visiting our website which covers about 2/5 + 1/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.