2 5 As A Mixed Number
Treneri
May 15, 2025 · 5 min read
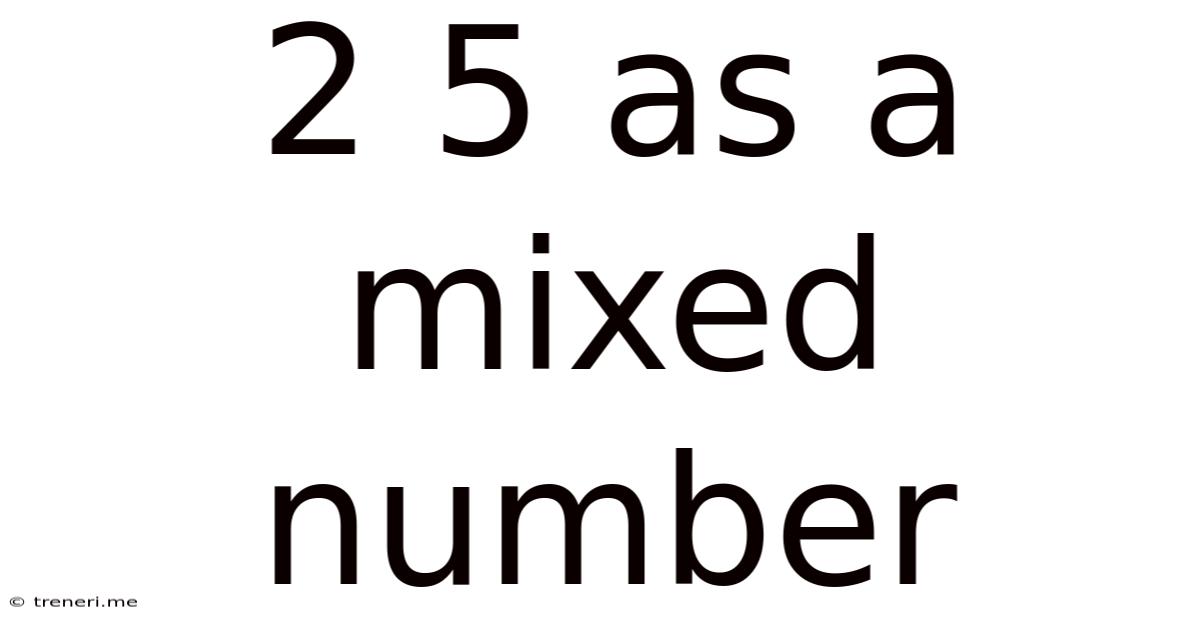
Table of Contents
2.5 as a Mixed Number: A Comprehensive Guide
Understanding fractions and decimals is fundamental to mathematics. Converting between different representations of numbers, like decimals to fractions and fractions to mixed numbers, is a crucial skill. This comprehensive guide will delve deep into converting the decimal 2.5 into a mixed number, explaining the process step-by-step and exploring related concepts. We'll also examine practical applications and provide helpful tips to master this conversion.
Understanding Mixed Numbers
Before we dive into the conversion, let's define a mixed number. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that's more than one whole unit.
Converting Decimals to Fractions: The Foundation
The process of converting 2.5 to a mixed number begins with understanding how to convert decimals to fractions. The key lies in recognizing the place value of each digit after the decimal point. In 2.5, the '.5' represents five-tenths, which can be written as the fraction 5/10.
Step-by-Step Conversion of 2.5 to a Fraction
-
Identify the decimal part: The decimal part of 2.5 is 0.5.
-
Write the decimal as a fraction: 0.5 can be written as 5/10. The digit 5 is in the tenths place, so the denominator is 10.
-
Simplify the fraction (if possible): Both 5 and 10 are divisible by 5. Simplifying the fraction, we get 1/2.
-
Combine with the whole number: The whole number part of 2.5 is 2. Therefore, combining the whole number and the simplified fraction, we get 2 ½.
2.5 as a Mixed Number: The Final Result
Therefore, the decimal 2.5 expressed as a mixed number is 2 ½. This means it's equivalent to two whole units and one-half of another unit.
Expanding on the Concept: Different Decimal Conversions
Let's examine how this conversion process applies to other decimals. This will solidify your understanding and build your confidence in tackling similar problems.
Example 1: Converting 3.75 to a Mixed Number
-
Decimal part: 0.75
-
Fraction: 75/100
-
Simplification: Both 75 and 100 are divisible by 25. This simplifies to 3/4.
-
Mixed number: 3 ¾
Example 2: Converting 1.2 to a Mixed Number
-
Decimal part: 0.2
-
Fraction: 2/10
-
Simplification: Dividing both by 2, we get 1/5.
-
Mixed number: 1 ⅕
Example 3: Converting 0.625 to a Mixed Number
-
Decimal part: 0.625
-
Fraction: 625/1000
-
Simplification: Dividing by 125, we get 5/8. Note that finding the greatest common divisor is essential for the most simplified fraction.
-
Mixed number: Since there's no whole number component, the answer remains 5/8 which is a proper fraction, not a mixed number.
Practical Applications of Mixed Numbers
Mixed numbers have practical applications in various fields:
-
Measurement: In carpentry, cooking, and many other trades, measurements are often expressed as mixed numbers (e.g., 2 ½ inches, 1 ¾ cups).
-
Time: Time can be expressed as mixed numbers (e.g., 1 ½ hours).
-
Data Analysis: In statistics, data may be represented using mixed numbers for easier interpretation.
-
Everyday Calculations: Many everyday calculations, such as dividing quantities of ingredients for cooking, benefit from the use of mixed numbers.
Advanced Techniques for Decimal to Fraction Conversion
While the above method works well for simple decimals, some decimals require more advanced techniques. Let's explore one such technique:
Dealing with Repeating Decimals
Converting repeating decimals to fractions involves a different approach. Repeating decimals have a sequence of digits that repeats infinitely. For example, 0.333... (0.3 repeating) is a repeating decimal.
Converting repeating decimals requires algebraic manipulation. This is a more advanced topic and is typically taught at a higher level of mathematics.
Troubleshooting Common Mistakes
When converting decimals to mixed numbers, certain common mistakes can occur:
-
Incorrect Simplification: Failing to simplify the fraction to its lowest terms. Always ensure you've found the greatest common divisor (GCD) of the numerator and denominator.
-
Incorrect Place Value: Misidentifying the place value of the digits after the decimal point. Pay close attention to tenths, hundredths, thousandths, and so on.
-
Ignoring the Whole Number: Forgetting to include the whole number part of the decimal in the final mixed number.
-
Improper Fractions: Sometimes students might accidentally end up with an improper fraction instead of a mixed number, requiring further conversion. Remember, in a mixed number, the fractional part must always be a proper fraction.
Tips for Mastering Decimal to Mixed Number Conversions
-
Practice Regularly: The key to mastering this skill is consistent practice. Work through numerous examples to build your understanding and confidence.
-
Understand Place Value: A solid grasp of place value is essential.
-
Use Online Resources: Many online calculators and tutorials can help you check your work and improve your understanding.
-
Break Down the Problem: Divide the problem into smaller, manageable steps. This makes the overall process less daunting.
-
Check Your Work: Always check your answer to ensure accuracy. You can convert the mixed number back to a decimal to verify the conversion.
Conclusion: 2.5, a Mixed Number Masterclass
Converting decimals to mixed numbers is a valuable skill applicable across various mathematical and real-world scenarios. Understanding the underlying principles, practicing regularly, and using the tips outlined in this guide will allow you to confidently tackle any decimal-to-mixed-number conversion problem. Remember, the conversion of 2.5 to a mixed number, 2 ½, is just one example of how this process works. By applying these principles, you can confidently handle a wide variety of decimal-to-fraction conversions. Mastering this skill lays a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Overtime Pay For 18 An Hour
May 15, 2025
-
How To Build Circles In Minecraft
May 15, 2025
-
What Size Rivet Do I Need
May 15, 2025
-
12 Ft By 36 Inch Pool Gallons
May 15, 2025
-
27 Is What Percent Of 40
May 15, 2025
Related Post
Thank you for visiting our website which covers about 2 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.