2 7 1 4 As A Fraction
Treneri
May 12, 2025 · 4 min read
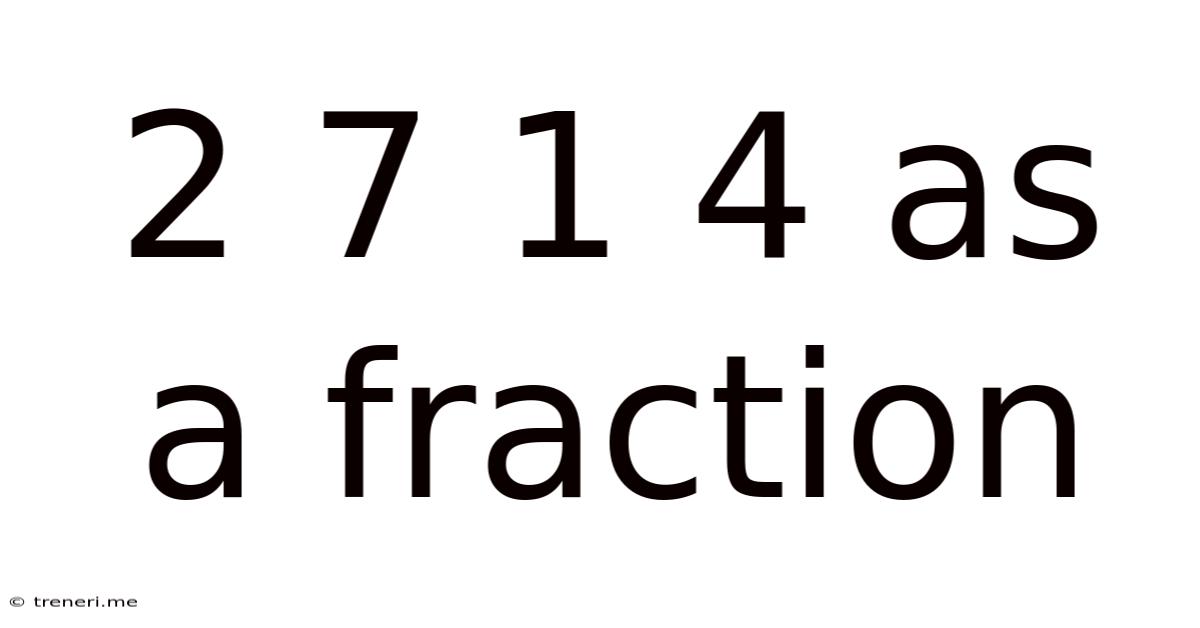
Table of Contents
2 7 1 4 as a Fraction: A Comprehensive Guide
Understanding how to convert mixed numbers and complex fractions into simpler forms is a fundamental skill in mathematics. This comprehensive guide delves into the process of converting the expression "2 7 1 4" into a fraction, explaining the underlying concepts and offering practical examples. We'll explore different approaches, ensuring a clear and thorough understanding of this seemingly complex mathematical operation.
Understanding the Expression: 2 7 1 4
The expression "2 7 1 4" isn't a standard mathematical notation. It likely represents a mixed number or a complex fraction. The most plausible interpretation is that it signifies a combination of whole numbers and fractions, perhaps something like a mixed number with a nested fraction. We'll address several interpretations to clarify the process.
Interpretation 1: A Mixed Number with a Nested Fraction
This interpretation assumes "2 7 1 4" represents the mixed number 2 and 7/ (1 + 4/x) , where 'x' is an unknown denominator. Without further information, we can't precisely determine the value of 'x'. We'll need to make an assumption for x.
Let's assume a potential meaning to give a context. We'll assume that it was a typo, and the actual expression was meant to be: 2 7/14
Converting 2 7/14 to an Improper Fraction:
- Multiply the whole number by the denominator: 2 * 14 = 28
- Add the numerator: 28 + 7 = 35
- Keep the same denominator: 14
- The improper fraction is: 35/14
Simplifying the Improper Fraction:
We can simplify 35/14 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 7:
35 ÷ 7 = 5 14 ÷ 7 = 2
Therefore, the simplified fraction is 5/2
Interpretation 2: A Complex Fraction
Another interpretation is that "2 7 1 4" represents a complex fraction, structured like this:
2 + 7 / (1 + 4)
Solving the Complex Fraction:
- Solve the Parentheses: 1 + 4 = 5
- Perform the Division: 7 / 5 = 1.4 or 7/5
- Perform the Addition: 2 + 1.4 = 3.4 or 2 + 7/5 = 17/5
This gives us the decimal result of 3.4 or the fraction 17/5. It is crucial to remember that the interpretation of this expression highly depends on the context or original intention.
Interpretation 3: Concatenation of Numbers
While less likely in a mathematical context, it's possible "2 7 1 4" is a concatenation of numbers, representing the improper fraction 2714/1. This fraction can be simplified if there's a common divisor between the numerator and the denominator. Since the denominator is 1, simplification isn't necessary, making 2714/1 = 2714.
Importance of Clarifying Mathematical Notation
These examples highlight the critical role of clear mathematical notation. Ambiguity can lead to vastly different results. Using parentheses, clear fractions, and proper formatting significantly reduces the chances of misinterpretations. If you encounter such expressions, seek clarification on the intended meaning.
Practical Application of Fraction Conversion
Converting fractions and mixed numbers is crucial in various fields:
- Baking and Cooking: Recipes frequently use fractions for precise ingredient measurements.
- Construction and Engineering: Accurate measurements are paramount, demanding proficiency in fractional calculations.
- Finance: Calculating interest, proportions, and ratios in financial calculations regularly involves fractions.
- Computer Science: Representing data structures, algorithms, and memory allocation frequently involves fractional concepts.
Advanced Concepts Related to Fractions
Understanding fractions goes beyond basic conversions. Here are some related advanced concepts:
- Continued Fractions: These are expressions where the numerator is a whole number plus a fraction, where the denominator is a whole number plus a fraction, and so on. Continued fractions can represent irrational numbers with remarkable accuracy.
- Partial Fractions: A technique to decompose a complex rational function into simpler fractions for easier integration in Calculus.
- Fraction Decomposition: Breaking down a complex fraction into the sum or difference of simpler fractions.
Conclusion: The Importance of Precise Mathematical Communication
The conversion of "2 7 1 4" as a fraction depends heavily on the correct interpretation of this ambiguous notation. The various interpretations demonstrate the importance of using clear and unambiguous mathematical notation to avoid confusion and ensure accurate results. Whether interpreting it as a mixed number, a complex fraction, or simply a concatenation of numbers, consistent mathematical principles allow us to approach the problem effectively. Mastering the techniques discussed here is valuable for various applications and lays a solid foundation for more advanced mathematical concepts. Always prioritize clear and accurate mathematical notation to foster understanding and prevent errors. Remember to utilize parenthesis to avoid ambiguity and ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
How Many Weeks In 35 Days
May 12, 2025
-
Un Terreno De 10 Por 20 Cuantos Metros Cuadrados Tiene
May 12, 2025
-
What Is A Good Time For An Olympic Triathlon
May 12, 2025
-
How Many Hours Is 500 Days
May 12, 2025
-
5 Out Of 21 As A Percentage
May 12, 2025
Related Post
Thank you for visiting our website which covers about 2 7 1 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.