2/9 + 5/9 As A Fraction
Treneri
May 14, 2025 · 5 min read
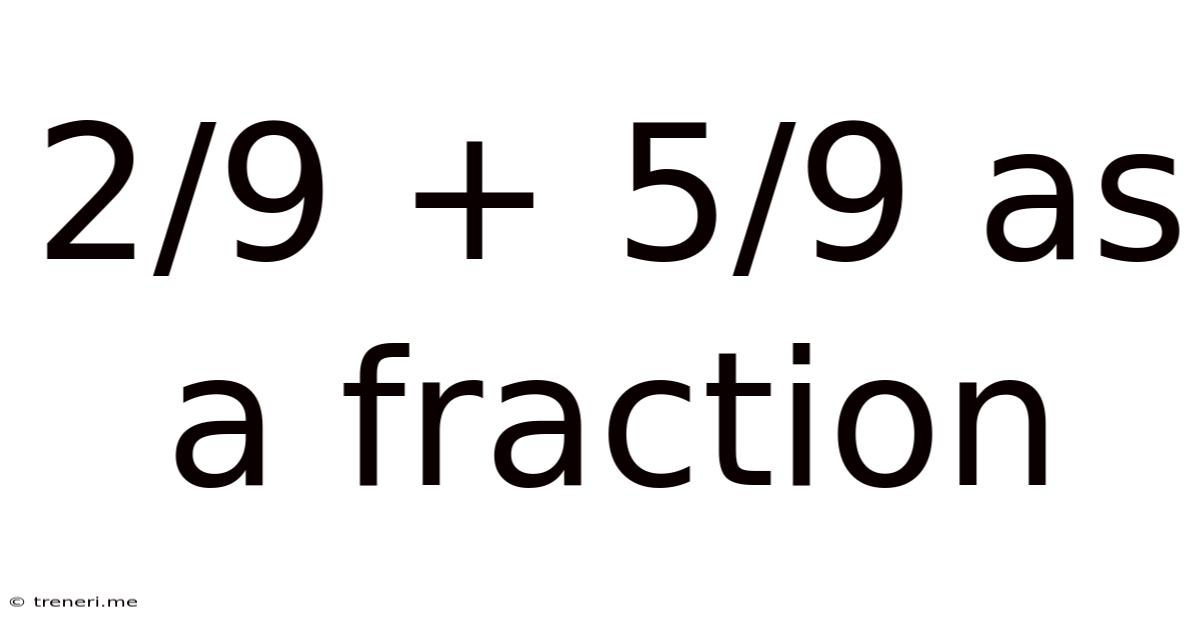
Table of Contents
2/9 + 5/9 as a Fraction: A Comprehensive Guide
Adding fractions might seem daunting at first, but with a structured approach, it becomes straightforward. This article delves into the seemingly simple addition of 2/9 + 5/9, providing a comprehensive explanation that goes beyond the immediate answer. We will explore the underlying concepts, demonstrate various methods, and discuss the broader implications for understanding fraction arithmetic. This will be useful not just for students learning fractions, but also for anyone wanting a refresher on fundamental mathematical concepts.
Understanding Fractions: A Quick Recap
Before tackling the addition, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
In our example, 2/9 and 5/9, both fractions share the same denominator (9). This is crucial for simplifying the addition process. The denominator signifies that the whole is divided into nine equal parts. 2/9 represents two of those nine parts, and 5/9 represents five of those same nine parts.
Adding Fractions with the Same Denominator
When adding fractions with the same denominator, the process is remarkably simple. We only need to add the numerators while keeping the denominator consistent. Let's apply this to our problem:
2/9 + 5/9 = (2 + 5)/9 = 7/9
The sum of the numerators (2 + 5 = 7) becomes the new numerator, while the common denominator (9) remains unchanged. Therefore, 2/9 + 5/9 equals 7/9. This represents seven out of nine equal parts of the whole.
Visualizing the Addition
Visual representations are incredibly helpful in grasping the concept of fraction addition. Imagine a pizza cut into nine equal slices.
- 2/9: You have two slices.
- 5/9: You receive five more slices.
- Total: You now possess seven slices (7/9) of the pizza.
This visual analogy reinforces the idea that we're simply combining parts of the same whole without altering the size of those parts.
Why the Denominator Remains Constant
The denominator represents the size or type of the parts we're working with. Since both fractions, 2/9 and 5/9, refer to the same size of parts (ninths), adding them doesn't change the size of the parts. We're only increasing the number of parts we have. Changing the denominator would be like comparing apples and oranges – the parts are fundamentally different.
Extending the Concept: Adding More Fractions with the Same Denominator
The principle remains the same when adding more than two fractions with a common denominator. Simply add all the numerators and retain the shared denominator. For instance:
1/12 + 5/12 + 2/12 = (1 + 5 + 2)/12 = 8/12
Note that this result (8/12) can be further simplified (explained in the next section).
Simplifying Fractions
Fractions should always be expressed in their simplest form. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's consider an example: We found that 1/12 + 5/12 + 2/12 = 8/12. To simplify 8/12, we need to find the GCD of 8 and 12. The GCD of 8 and 12 is 4. Therefore:
8/12 = (8 ÷ 4) / (12 ÷ 4) = 2/3
Therefore, the simplified answer is 2/3. This represents two parts out of three equal parts of a whole.
In the initial problem (2/9 + 5/9 = 7/9), the fraction is already in its simplest form because the GCD of 7 and 9 is 1.
Adding Fractions with Different Denominators
The process becomes slightly more complex when dealing with fractions that have different denominators. In such cases, we need to find a common denominator before adding the numerators. This involves finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators.
For example, let's add 1/3 + 1/4.
- Find the LCM: The LCM of 3 and 4 is 12.
- Convert Fractions: Convert both fractions to have a denominator of 12.
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 1/4 = (1 x 3) / (4 x 3) = 3/12
- Add Fractions: Add the numerators while keeping the common denominator:
- 4/12 + 3/12 = (4 + 3)/12 = 7/12
Real-World Applications of Fraction Addition
Understanding fraction addition is crucial in various real-world scenarios:
- Cooking and Baking: Following recipes often involves combining fractional quantities of ingredients.
- Construction and Engineering: Precise measurements and calculations in construction require accurate fraction addition.
- Finance: Handling portions of investments or calculating interest often involves fractional arithmetic.
- Science: Many scientific measurements and calculations utilize fractions.
Troubleshooting Common Mistakes
- Forgetting to find a common denominator: This is the most frequent error when adding fractions with different denominators. Always ensure both fractions have the same denominator before adding the numerators.
- Incorrectly simplifying fractions: Ensure you find the greatest common divisor when simplifying. Failing to do so will result in an unsimplified answer.
- Adding denominators: Remember, you only add the numerators; the denominator remains constant when the denominators are the same.
Conclusion: Mastering Fraction Addition
Adding fractions, especially those with the same denominator, is a fundamental arithmetic skill. By understanding the underlying concepts, employing visualization techniques, and practicing regularly, you can master this essential aspect of mathematics. The simple addition of 2/9 + 5/9, as explored in this comprehensive guide, serves as a stepping stone to tackling more complex fraction problems and further solidifying your understanding of fractional arithmetic. Remember to always simplify your answer to its simplest form for a complete and accurate solution. The ability to perform these calculations efficiently opens doors to more advanced mathematical concepts and enhances your problem-solving skills across numerous fields.
Latest Posts
Latest Posts
-
Cuantos Metros Tiene Una Hectarea De Tierra
May 15, 2025
-
90 Days From March 5th 2024
May 15, 2025
-
Formula For Mass Of A Cube
May 15, 2025
-
3 Quarts Equals How Many Cups Of Water
May 15, 2025
-
E To The What Equals 0
May 15, 2025
Related Post
Thank you for visiting our website which covers about 2/9 + 5/9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.