2 Divided By 5/6 As A Fraction
Treneri
May 13, 2025 · 5 min read
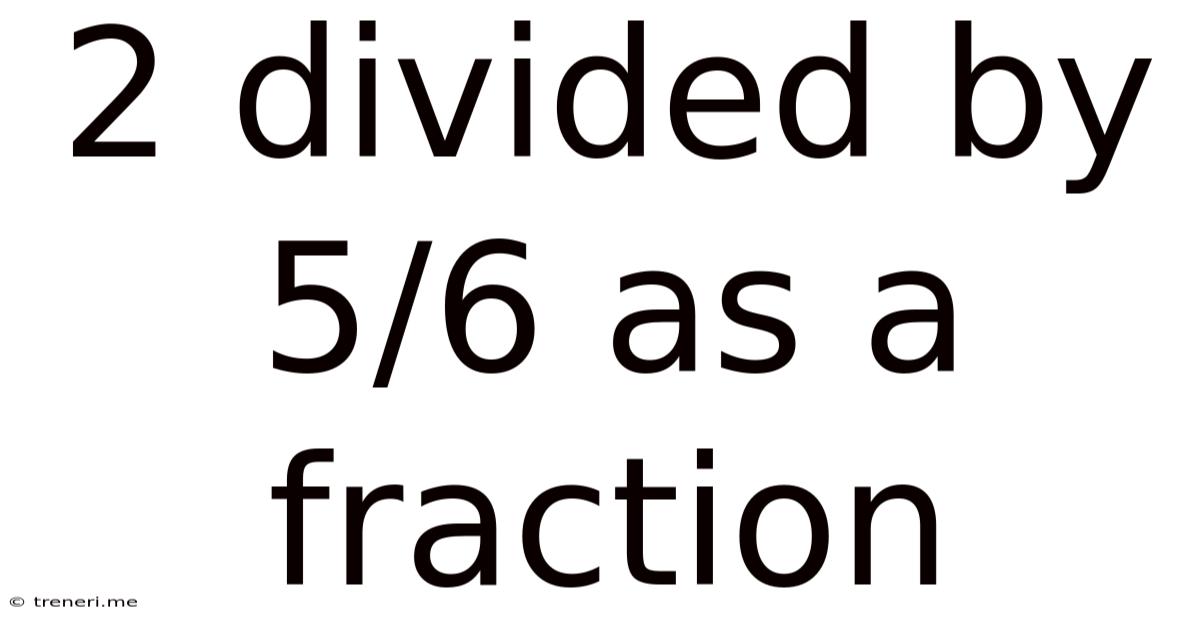
Table of Contents
2 Divided by 5/6 as a Fraction: A Comprehensive Guide
This article will delve into the seemingly simple yet often confusing problem of dividing 2 by the fraction 5/6. We'll explore multiple methods to solve this, emphasizing the underlying mathematical principles and providing a step-by-step breakdown for easy understanding. This will be particularly beneficial for students learning about fractions and division, as well as anyone looking to refresh their knowledge of basic arithmetic. We'll also touch upon the importance of understanding fraction division in real-world applications.
Understanding Fraction Division
Before we tackle the specific problem, let's establish a solid foundation in dividing fractions. The key concept to remember is that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 5/6 is 6/5.
This principle is crucial because it transforms a division problem into a simpler multiplication problem, which is often easier to solve. This simplification makes complex fraction calculations manageable.
Key takeaway: Dividing by a fraction is equivalent to multiplying by its reciprocal.
Method 1: Using the Reciprocal Method
This is the most common and arguably the easiest method for solving 2 divided by 5/6.
Step 1: Rewrite the problem
Rewrite the problem as a multiplication problem by replacing the division sign with a multiplication sign and flipping the second fraction (the divisor). This converts 2 ÷ 5/6 into 2 x 6/5.
Step 2: Convert the whole number to a fraction
It's often easier to work with fractions consistently. Convert the whole number 2 into a fraction with a denominator of 1: 2/1. Our problem now becomes 2/1 x 6/5.
Step 3: Multiply the numerators and denominators
Multiply the numerators together (top numbers) and the denominators together (bottom numbers):
(2 x 6) / (1 x 5) = 12/5
Step 4: Simplify the fraction (if necessary)
In this case, 12/5 is an improper fraction (the numerator is larger than the denominator). We can simplify this into a mixed number:
12 ÷ 5 = 2 with a remainder of 2. Therefore, 12/5 can be expressed as 2 2/5.
Therefore, 2 divided by 5/6 equals 12/5 or 2 2/5.
Method 2: The "Keep, Change, Flip" Method
This is a mnemonic device often used to help students remember the process of dividing fractions. It's essentially a shorthand version of the reciprocal method.
Keep: Keep the first number (the dividend) as it is. In our case, this is 2.
Change: Change the division sign (÷) to a multiplication sign (x).
Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of 5/6 is 6/5.
So, 2 ÷ 5/6 becomes 2 x 6/5. From here, you follow the same steps as in Method 1: convert 2 to 2/1, multiply the numerators and denominators, and simplify the resulting fraction.
Method 3: Visual Representation using Area Models
While less efficient for complex problems, visualizing the division with area models can enhance understanding, especially for beginners. Imagine a rectangle representing 2 whole units. To divide this by 5/6, we need to figure out how many 5/6 units fit into 2 units.
This method requires drawing and subdividing rectangles, making it less practical for large numbers but beneficial for conceptual understanding. It visually demonstrates the concept of dividing a whole into fractional parts.
Real-World Applications of Fraction Division
Understanding fraction division is crucial in many real-world scenarios:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. If a recipe calls for 2/3 cup of flour and you want to make a double batch, you need to multiply by 2 (or divide the total amount by 1/2 if you're halving the recipe), which involves fraction division or multiplication.
-
Sewing and Tailoring: Fabric cutting frequently involves fractional measurements. Dividing a length of fabric into fractional pieces requires proficiency in fraction division.
-
Construction and Engineering: Precise measurements are vital in these fields. Dividing lengths, volumes, and areas often involves fractions.
-
Finance and Budgeting: Dividing budgets, calculating portions of investments, and understanding percentages (which are essentially fractions) all rely on understanding fraction division.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing fractions:
-
Forgetting to flip the second fraction: This is the most frequent error. Always remember to find the reciprocal of the divisor before multiplying.
-
Incorrect multiplication of fractions: Make sure you multiply numerators by numerators and denominators by denominators.
-
Failure to simplify the final answer: Always simplify your answer to its lowest terms. Improper fractions should be converted to mixed numbers for ease of understanding.
-
Misunderstanding the concept of reciprocals: Ensure you have a strong grasp of what a reciprocal is and how to find it.
Advanced Concepts and Extensions
While this article focused on a basic example, the principles extend to more complex problems involving mixed numbers, decimals, and even algebraic expressions. Mastering the fundamentals of dividing fractions is the foundation for tackling these more advanced calculations.
Further exploration could include:
-
Dividing mixed numbers: This involves converting mixed numbers to improper fractions before applying the reciprocal method.
-
Dividing fractions with variables: This introduces algebraic concepts, requiring understanding of fraction manipulation and simplification within algebraic expressions.
-
Applying fraction division in more complex word problems: These problems require careful reading, identifying the relevant fractions, and choosing the appropriate method for solving the problem.
Conclusion
Dividing 2 by 5/6, resulting in 12/5 or 2 2/5, might appear straightforward, yet a solid understanding of the underlying concepts is crucial for more complex calculations. By mastering the reciprocal method, the "Keep, Change, Flip" mnemonic, and even the visual representation using area models, you'll build a strong foundation in fraction division, applicable across various mathematical and real-world contexts. Remember to practice regularly to solidify your understanding and avoid common pitfalls. The more you practice, the more comfortable and confident you'll become with fractional arithmetic.
Latest Posts
Latest Posts
-
How Much Time Until 10 30
May 13, 2025
-
500 Sq M To Sq Ft
May 13, 2025
-
What Is The Equivalent Fraction Of 2 6
May 13, 2025
-
7 Is 5 Percent Of What Number
May 13, 2025
-
What Is A Split In Track
May 13, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By 5/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.